Question Number 164879 by ajfour last updated on 22/Jan/22

Commented by ajfour last updated on 22/Jan/22

$${Find}\:{coordinates}\:{of}\:{A},\:{B},\:{C},\:{T} \\ $$$${if}\:{O}\:{is}\:{center}\:{of}\:{the}\:{regular} \\ $$$${tetrahedron},\:{and}\:{side}\:{of}\:{tetrahedron} \\ $$$${be}\:{a}\:\left({or}\:{unity}\right). \\ $$
Answered by ajfour last updated on 22/Jan/22
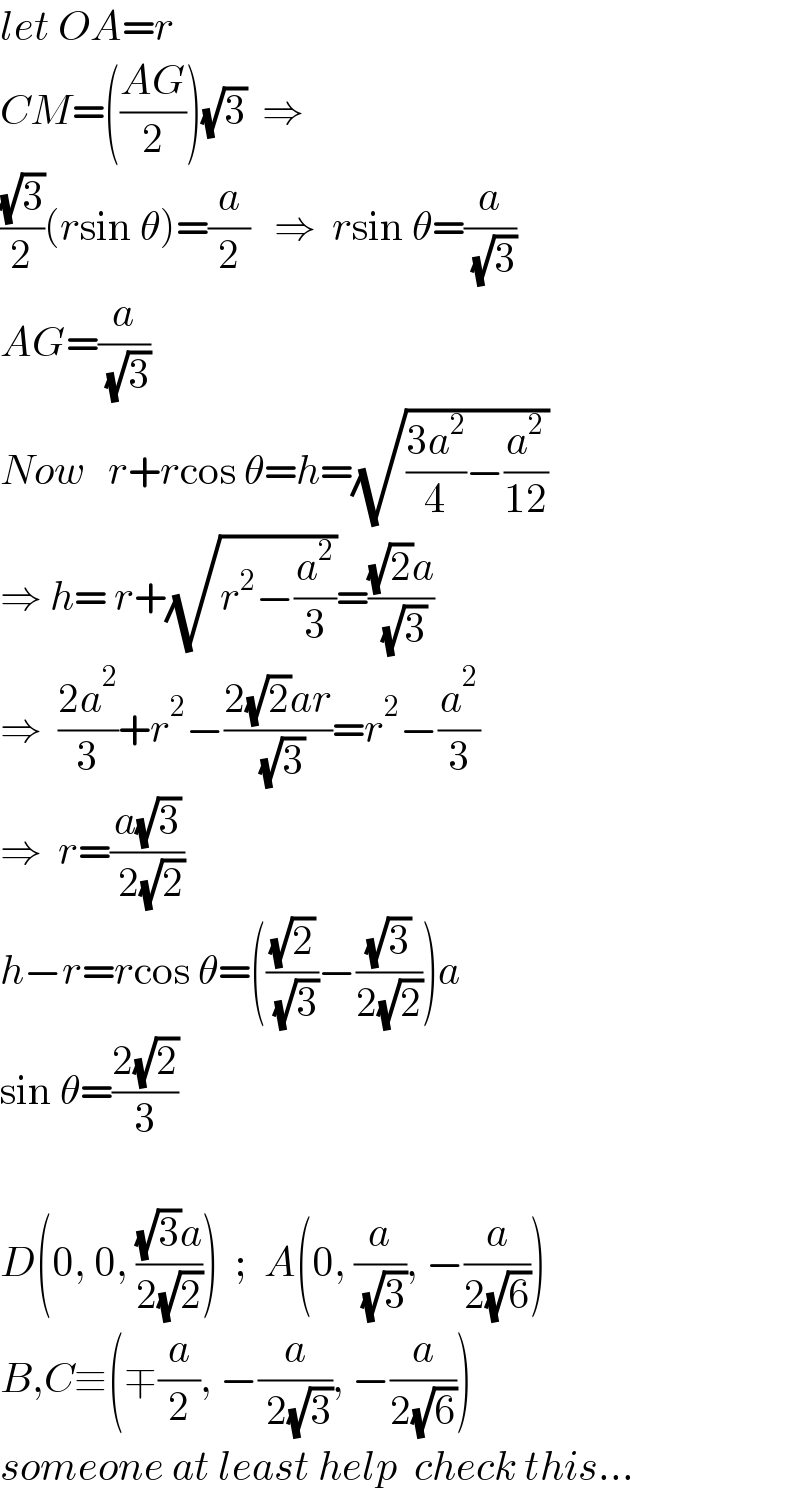
$${let}\:{OA}={r} \\ $$$${CM}=\left(\frac{{AG}}{\mathrm{2}}\right)\sqrt{\mathrm{3}}\:\:\Rightarrow \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({r}\mathrm{sin}\:\theta\right)=\frac{{a}}{\mathrm{2}}\:\:\:\Rightarrow\:\:{r}\mathrm{sin}\:\theta=\frac{{a}}{\:\sqrt{\mathrm{3}}} \\ $$$${AG}=\frac{{a}}{\:\sqrt{\mathrm{3}}} \\ $$$${Now}\:\:\:{r}+{r}\mathrm{cos}\:\theta={h}=\sqrt{\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{4}}−\frac{{a}^{\mathrm{2}} }{\mathrm{12}}} \\ $$$$\Rightarrow\:{h}=\:{r}+\sqrt{{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{3}}}=\frac{\sqrt{\mathrm{2}}{a}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{3}}+{r}^{\mathrm{2}} −\frac{\mathrm{2}\sqrt{\mathrm{2}}{ar}}{\:\sqrt{\mathrm{3}}}={r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\:{r}=\frac{{a}\sqrt{\mathrm{3}}}{\:\mathrm{2}\sqrt{\mathrm{2}}}\:\: \\ $$$${h}−{r}={r}\mathrm{cos}\:\theta=\left(\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}}}\right){a} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$ \\ $$$${D}\left(\mathrm{0},\:\mathrm{0},\:\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\:\:;\:\:{A}\left(\mathrm{0},\:\frac{{a}}{\:\sqrt{\mathrm{3}}},\:−\frac{{a}}{\mathrm{2}\sqrt{\mathrm{6}}}\right) \\ $$$${B},{C}\equiv\left(\mp\frac{{a}}{\mathrm{2}},\:−\frac{{a}}{\:\mathrm{2}\sqrt{\mathrm{3}}},\:−\frac{{a}}{\mathrm{2}\sqrt{\mathrm{6}}}\right) \\ $$$${someone}\:{at}\:{least}\:{help}\:\:{check}\:{this}… \\ $$
Commented by mr W last updated on 23/Jan/22

$${it}'{s}\:{perfect}\:{sir}! \\ $$
