Question Number 164923 by mathlove last updated on 23/Jan/22
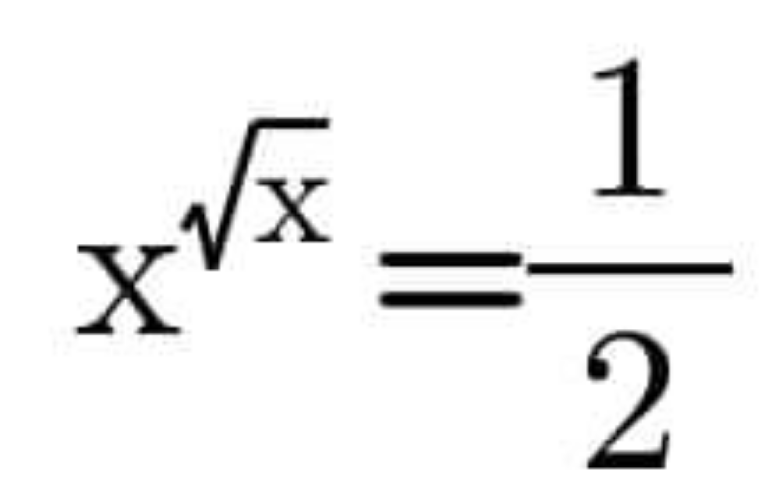
Commented by MJS_new last updated on 24/Jan/22
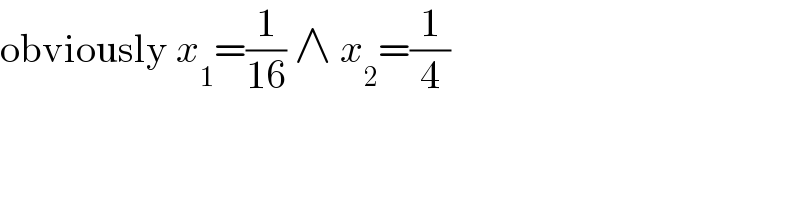
$$\mathrm{obviously}\:{x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{16}}\:\wedge\:{x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by Eulerian last updated on 23/Jan/22

$$\:\boldsymbol{\mathrm{Solution}}: \\ $$$$\:\mathrm{let}:\:\sqrt{\mathrm{x}}\:=\:\mathrm{k}\:\:\rightarrow\:\:\mathrm{x}\:=\:\mathrm{k}^{\mathrm{2}} \\ $$$$\: \\ $$$$\:\therefore \\ $$$$\:\mathrm{k}^{\mathrm{2k}} \:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\mathrm{k}^{\mathrm{k}} \:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\:\mathrm{k}\centerdot\mathrm{ln}\left(\mathrm{k}\right)\:=\:−\mathrm{ln}\left(\sqrt{\mathrm{2}}\right) \\ $$$$\:\mathrm{By}\:\mathrm{applying}\:\mathrm{the}\:\mathrm{productlog}\:\mathrm{on}\:\mathrm{both}\:\mathrm{sides}: \\ $$$$\:\mathrm{ln}\left(\mathrm{k}\right)\:=\:\mathrm{W}\left(−\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\right) \\ $$$$\:\mathrm{k}\:=\:\mathrm{e}^{\mathrm{W}\left(−\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\right)} \:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\therefore \\ $$$$\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 23/Jan/22
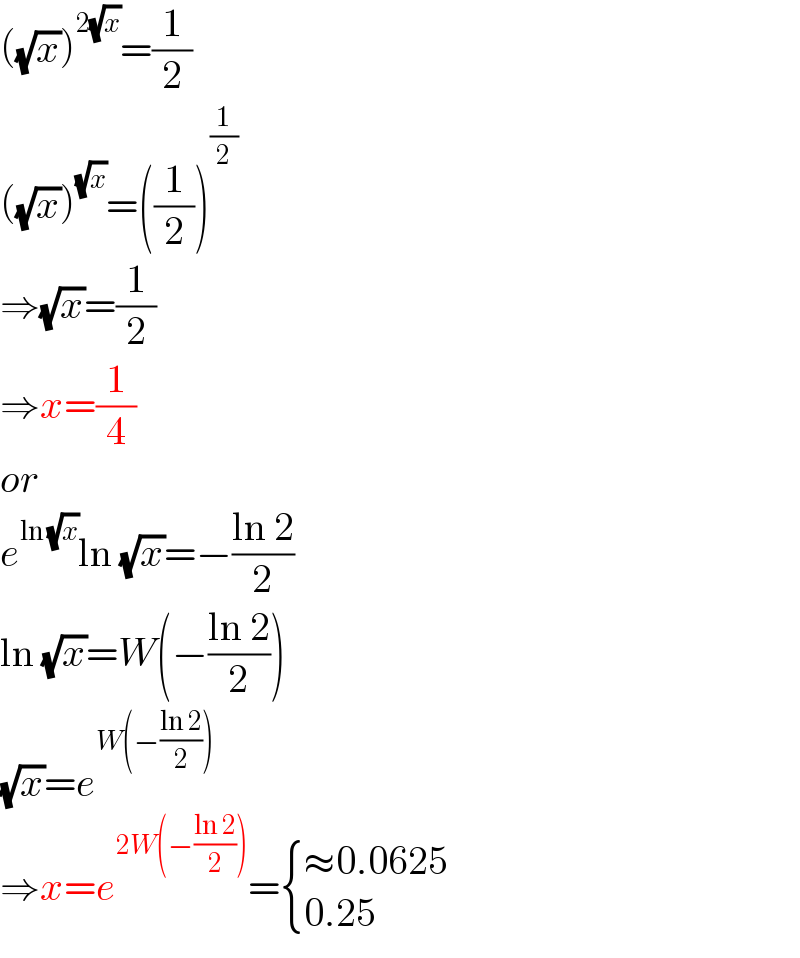
$$\left(\sqrt{{x}}\right)^{\mathrm{2}\sqrt{{x}}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\sqrt{{x}}\right)^{\sqrt{{x}}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow\sqrt{{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${or} \\ $$$${e}^{\mathrm{ln}\:\sqrt{{x}}} \mathrm{ln}\:\sqrt{{x}}=−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$$\mathrm{ln}\:\sqrt{{x}}={W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\sqrt{{x}}={e}^{{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow{x}={e}^{\mathrm{2}{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)} =\begin{cases}{\approx\mathrm{0}.\mathrm{0625}}\\{\mathrm{0}.\mathrm{25}}\end{cases} \\ $$
