Question Number 164941 by ajfour last updated on 23/Jan/22
Commented by ajfour last updated on 23/Jan/22

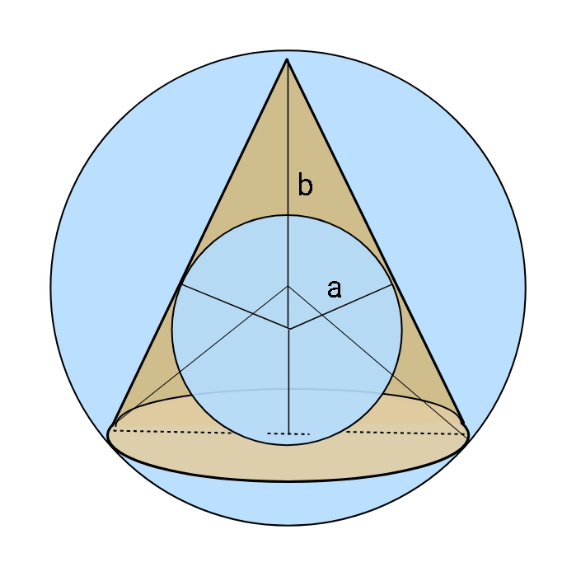
$${If}\:{radii}\:{of}\:{inscribed}\:{and}\:{circum}- \\ $$$${scribed}\:{spheres}\:{are}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}},\:{find} \\ $$$${height}\:{and}\:{radius}\:{of}\:{cone}. \\ $$
Answered by mr W last updated on 23/Jan/22
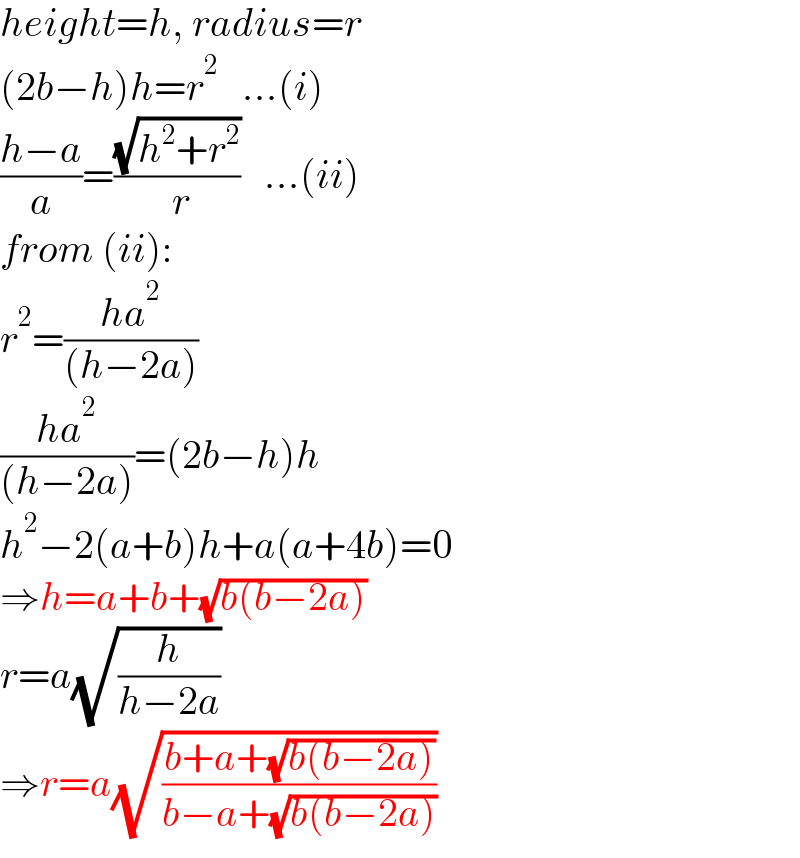
$${height}={h},\:{radius}={r} \\ $$$$\left(\mathrm{2}{b}−{h}\right){h}={r}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\frac{{h}−{a}}{{a}}=\frac{\sqrt{{h}^{\mathrm{2}} +{r}^{\mathrm{2}} }}{\:{r}}\:\:\:…\left({ii}\right) \\ $$$${from}\:\left({ii}\right): \\ $$$${r}^{\mathrm{2}} =\frac{{ha}^{\mathrm{2}} }{\left({h}−\mathrm{2}{a}\right)} \\ $$$$\frac{{ha}^{\mathrm{2}} }{\left({h}−\mathrm{2}{a}\right)}=\left(\mathrm{2}{b}−{h}\right){h} \\ $$$${h}^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\right){h}+{a}\left({a}+\mathrm{4}{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{h}={a}+{b}+\sqrt{{b}\left({b}−\mathrm{2}{a}\right)} \\ $$$${r}={a}\sqrt{\frac{{h}}{{h}−\mathrm{2}{a}}} \\ $$$$\Rightarrow{r}={a}\sqrt{\frac{{b}+{a}+\sqrt{{b}\left({b}−\mathrm{2}{a}\right)}}{{b}−{a}+\sqrt{{b}\left({b}−\mathrm{2}{a}\right)}}} \\ $$
Commented by Tawa11 last updated on 23/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by ajfour last updated on 24/Jan/22
$${Very}\:{straight}\:{n}\:{pragmatic}, \\ $$$${really}\:{great}\:{sir}.\:{Thank}\:{you}. \\ $$
