Menu Close

Question-164985

Tinku Tara 0 Comments
Pin




Question Number 164985 by cortano1 last updated on 24/Jan/22
Answered by Eulerian last updated on 24/Jan/22
Solution: 3∙((log^2 (x))/(log^2 (2))) − 1 − 9∙((log^2 (2))/(log^2 (x))) = 25 let: k = ((log^2 (x))/(log^2 (2))) ∴ 3k − (9/k) = 26 3k^2 −26k−9 = 0 By quadratic formula: k = ((26±(√(26^2 −4(3)(−9))))/(2(3))) = ((26±28)/6) ∴ k_1 = 9 k_2 = −(1/3) By substituting back: log^2 (x) = 9∙log^2 (2) log(x) = 3∙log(2) x = 8 and log(x) = ((i(√3))/( 3))∙log(2) x = 2^((i(√3))/3)
$$\: \\ $$$$\:\boldsymbol{\mathrm{Solution}}: \\ $$$$\:\mathrm{3}\centerdot\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{log}^{\mathrm{2}} \left(\mathrm{2}\right)}\:−\:\mathrm{1}\:−\:\mathrm{9}\centerdot\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{log}^{\mathrm{2}} \left(\mathrm{x}\right)}\:=\:\mathrm{25} \\ $$$$\: \\ $$$$\:\mathrm{let}:\:\mathrm{k}\:=\:\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{log}^{\mathrm{2}} \left(\mathrm{2}\right)} \\ $$$$\:\therefore \\ $$$$\:\mathrm{3k}\:−\:\frac{\mathrm{9}}{\mathrm{k}}\:=\:\mathrm{26} \\ $$$$\:\mathrm{3k}^{\mathrm{2}} −\mathrm{26k}−\mathrm{9}\:=\:\mathrm{0} \\ $$$$\: \\ $$$$\:\mathrm{By}\:\mathrm{quadratic}\:\mathrm{formula}: \\ $$$$\:\mathrm{k}\:=\:\frac{\mathrm{26}\pm\sqrt{\mathrm{26}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{3}\right)\left(−\mathrm{9}\right)}}{\mathrm{2}\left(\mathrm{3}\right)}\:=\:\frac{\mathrm{26}\pm\mathrm{28}}{\mathrm{6}} \\ $$$$\:\therefore \\ $$$$\:\mathrm{k}_{\mathrm{1}} \:=\:\mathrm{9}\:\: \\ $$$$\:\mathrm{k}_{\mathrm{2}} \:=\:−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\: \\ $$$$\:\mathrm{By}\:\mathrm{substituting}\:\mathrm{back}: \\ $$$$\:\mathrm{log}^{\mathrm{2}} \left(\mathrm{x}\right)\:=\:\mathrm{9}\centerdot\mathrm{log}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\:\mathrm{log}\left(\mathrm{x}\right)\:=\:\mathrm{3}\centerdot\mathrm{log}\left(\mathrm{2}\right) \\ $$$$\:\mathrm{x}\:=\:\mathrm{8} \\ $$$$\: \\ $$$$\:\mathrm{and} \\ $$$$\: \\ $$$$\:\mathrm{log}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\:\mathrm{3}}\centerdot\mathrm{log}\left(\mathrm{2}\right) \\ $$$$\:\mathrm{x}\:=\:\mathrm{2}^{\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{3}}} \\ $$$$\: \\ $$
Answered by alephzero last updated on 24/Jan/22
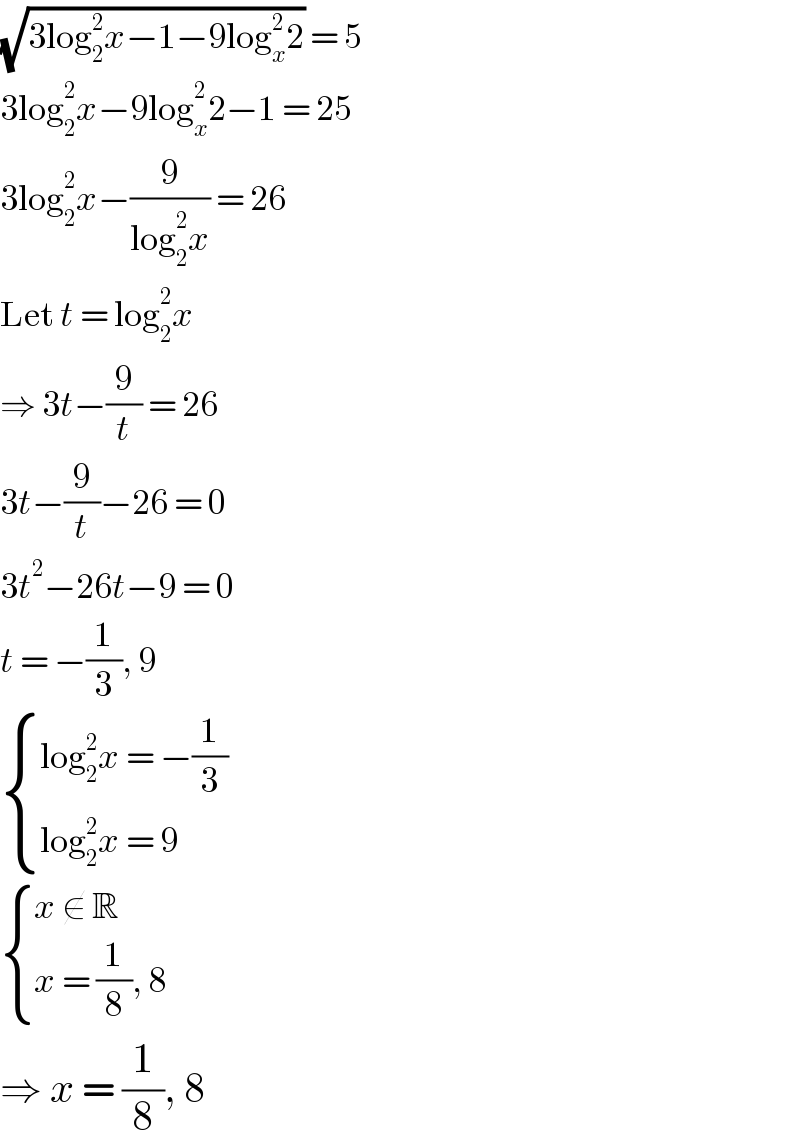
(√(3log_2 ^2 x−1−9log_x ^2 2)) = 5 3log_2 ^2 x−9log_x ^2 2−1 = 25 3log_2 ^2 x−(9/(log_2 ^2 x)) = 26 Let t = log_2 ^2 x ⇒ 3t−(9/t) = 26 3t−(9/t)−26 = 0 3t^2 −26t−9 = 0 t = −(1/3), 9 { ((log_2 ^2 x = −(1/3))),((log_2 ^2 x = 9)) :} { ((x ∉ R)),((x = (1/8), 8)) :} ⇒ x = (1/8), 8
$$\sqrt{\mathrm{3log}_{\mathrm{2}} ^{\mathrm{2}} {x}−\mathrm{1}−\mathrm{9log}_{{x}} ^{\mathrm{2}} \mathrm{2}}\:=\:\mathrm{5} \\ $$$$\mathrm{3log}_{\mathrm{2}} ^{\mathrm{2}} {x}−\mathrm{9log}_{{x}} ^{\mathrm{2}} \mathrm{2}−\mathrm{1}\:=\:\mathrm{25} \\ $$$$\mathrm{3log}_{\mathrm{2}} ^{\mathrm{2}} {x}−\frac{\mathrm{9}}{\mathrm{log}_{\mathrm{2}} ^{\mathrm{2}} {x}}\:=\:\mathrm{26} \\ $$$$\mathrm{Let}\:{t}\:=\:\mathrm{log}_{\mathrm{2}} ^{\mathrm{2}} {x} \\ $$$$\Rightarrow\:\mathrm{3}{t}−\frac{\mathrm{9}}{{t}}\:=\:\mathrm{26} \\ $$$$\mathrm{3}{t}−\frac{\mathrm{9}}{{t}}−\mathrm{26}\:=\:\mathrm{0} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} −\mathrm{26}{t}−\mathrm{9}\:=\:\mathrm{0} \\ $$$${t}\:=\:−\frac{\mathrm{1}}{\mathrm{3}},\:\mathrm{9} \\ $$$$\begin{cases}{\mathrm{log}_{\mathrm{2}} ^{\mathrm{2}} {x}\:=\:−\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{log}_{\mathrm{2}} ^{\mathrm{2}} {x}\:=\:\mathrm{9}}\end{cases} \\ $$$$\begin{cases}{{x}\:\notin\:\mathbb{R}}\\{{x}\:=\:\frac{\mathrm{1}}{\mathrm{8}},\:\mathrm{8}}\end{cases} \\ $$$$\Rightarrow\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{8}},\:\mathrm{8} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *