Menu Close

Question-164995

Tinku Tara 0 Comments
Pin




Question Number 164995 by Mathematification last updated on 24/Jan/22
Answered by aleks041103 last updated on 25/Jan/22
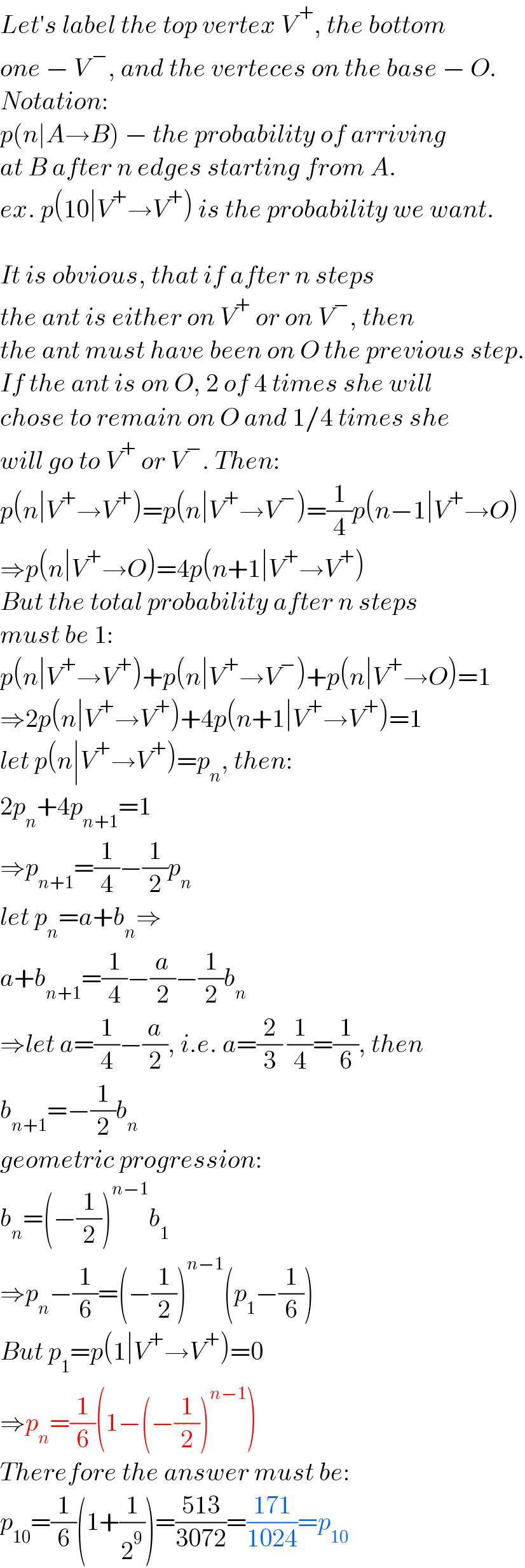
Let′s label the top vertex V^( +) , the bottom one − V^( −) , and the verteces on the base − O. Notation: p(n∣A→B) − the probability of arriving at B after n edges starting from A. ex. p(10∣V^+ →V^+ ) is the probability we want. It is obvious, that if after n steps the ant is either on V^+ or on V^− , then the ant must have been on O the previous step. If the ant is on O, 2 of 4 times she will chose to remain on O and 1/4 times she will go to V^+ or V^− . Then: p(n∣V^+ →V^+ )=p(n∣V^+ →V^− )=(1/4)p(n−1∣V^+ →O) ⇒p(n∣V^+ →O)=4p(n+1∣V^+ →V^+ ) But the total probability after n steps must be 1: p(n∣V^+ →V^+ )+p(n∣V^+ →V^− )+p(n∣V^+ →O)=1 ⇒2p(n∣V^+ →V^+ )+4p(n+1∣V^+ →V^+ )=1 let p(n∣V^+ →V^+ )=p_n , then: 2p_n +4p_(n+1) =1 ⇒p_(n+1) =(1/4)−(1/2)p_n let p_n =a+b_n ⇒ a+b_(n+1) =(1/4)−(a/2)−(1/2)b_n ⇒let a=(1/4)−(a/2), i.e. a=(2/3) (1/4)=(1/6), then b_(n+1) =−(1/2)b_n geometric progression: b_n =(−(1/2))^(n−1) b_1 ⇒p_n −(1/6)=(−(1/2))^(n−1) (p_1 −(1/6)) But p_1 =p(1∣V^+ →V^+ )=0 ⇒p_n =(1/6)(1−(−(1/2))^(n−1) ) Therefore the answer must be: p_(10) =(1/6)(1+(1/2^9 ))=((513)/(3072))=((171)/(1024))=p_(10)
$${Let}'{s}\:{label}\:{the}\:{top}\:{vertex}\:{V}^{\:+} ,\:{the}\:{bottom} \\ $$$${one}\:−\:{V}^{\:−} ,\:{and}\:{the}\:{verteces}\:{on}\:{the}\:{base}\:−\:{O}. \\ $$$${Notation}: \\ $$$${p}\left({n}\mid{A}\rightarrow{B}\right)\:−\:{the}\:{probability}\:{of}\:{arriving} \\ $$$${at}\:{B}\:{after}\:{n}\:{edges}\:{starting}\:{from}\:{A}. \\ $$$${ex}.\:{p}\left(\mathrm{10}\mid{V}^{+} \rightarrow{V}^{+} \right)\:{is}\:{the}\:{probability}\:{we}\:{want}. \\ $$$$ \\ $$$${It}\:{is}\:{obvious},\:{that}\:{if}\:{after}\:{n}\:{steps} \\ $$$${the}\:{ant}\:{is}\:{either}\:{on}\:{V}^{+} \:{or}\:{on}\:{V}^{−} ,\:{then} \\ $$$${the}\:{ant}\:{must}\:{have}\:{been}\:{on}\:{O}\:{the}\:{previous}\:{step}. \\ $$$${If}\:{the}\:{ant}\:{is}\:{on}\:{O},\:\mathrm{2}\:{of}\:\mathrm{4}\:{times}\:{she}\:{will} \\ $$$${chose}\:{to}\:{remain}\:{on}\:{O}\:{and}\:\mathrm{1}/\mathrm{4}\:{times}\:{she} \\ $$$${will}\:{go}\:{to}\:{V}^{+} \:{or}\:{V}^{−} .\:{Then}: \\ $$$${p}\left({n}\mid{V}^{+} \rightarrow{V}^{+} \right)={p}\left({n}\mid{V}^{+} \rightarrow{V}^{−} \right)=\frac{\mathrm{1}}{\mathrm{4}}{p}\left({n}−\mathrm{1}\mid{V}^{+} \rightarrow{O}\right) \\ $$$$\Rightarrow{p}\left({n}\mid{V}^{+} \rightarrow{O}\right)=\mathrm{4}{p}\left({n}+\mathrm{1}\mid{V}^{+} \rightarrow{V}^{+} \right) \\ $$$${But}\:{the}\:{total}\:{probability}\:{after}\:{n}\:{steps} \\ $$$${must}\:{be}\:\mathrm{1}: \\ $$$${p}\left({n}\mid{V}^{+} \rightarrow{V}^{+} \right)+{p}\left({n}\mid{V}^{+} \rightarrow{V}^{−} \right)+{p}\left({n}\mid{V}^{+} \rightarrow{O}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{p}\left({n}\mid{V}^{+} \rightarrow{V}^{+} \right)+\mathrm{4}{p}\left({n}+\mathrm{1}\mid{V}^{+} \rightarrow{V}^{+} \right)=\mathrm{1} \\ $$$${let}\:{p}\left({n}\mid{V}^{+} \rightarrow{V}^{+} \right)={p}_{{n}} ,\:{then}: \\ $$$$\mathrm{2}{p}_{{n}} +\mathrm{4}{p}_{{n}+\mathrm{1}} =\mathrm{1} \\ $$$$\Rightarrow{p}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{p}_{{n}} \\ $$$${let}\:{p}_{{n}} ={a}+{b}_{{n}} \Rightarrow \\ $$$${a}+{b}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}−\frac{{a}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{b}_{{n}} \\ $$$$\Rightarrow{let}\:{a}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{{a}}{\mathrm{2}},\:{i}.{e}.\:{a}=\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{6}},\:{then} \\ $$$${b}_{{n}+\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}{b}_{{n}} \\ $$$${geometric}\:{progression}: \\ $$$${b}_{{n}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} {b}_{\mathrm{1}} \\ $$$$\Rightarrow{p}_{{n}} −\frac{\mathrm{1}}{\mathrm{6}}=\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \left({p}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$${But}\:{p}_{\mathrm{1}} ={p}\left(\mathrm{1}\mid{V}^{+} \rightarrow{V}^{+} \right)=\mathrm{0} \\ $$$$\Rightarrow{p}_{{n}} =\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \right) \\ $$$${Therefore}\:{the}\:{answer}\:{must}\:{be}: \\ $$$${p}_{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{9}} }\right)=\frac{\mathrm{513}}{\mathrm{3072}}=\frac{\mathrm{171}}{\mathrm{1024}}={p}_{\mathrm{10}} \\ $$
Commented by aleks041103 last updated on 25/Jan/22
It is worth noting, that p_n →(1/6), when n→∞. This is connected to Markov′s rule that after enough random walks on a graph, the probability of being on any vertex is proportional to the number of edges connected to the given vertex. In our case all verteces have 4 edges connected to them, and therefore the probability is the same for all 6 verteces, i.e. it′s (1/6).
$${It}\:{is}\:{worth}\:{noting},\:{that}\:{p}_{{n}} \rightarrow\frac{\mathrm{1}}{\mathrm{6}},\:{when} \\ $$$${n}\rightarrow\infty.\:{This}\:{is}\:{connected}\:{to}\:{Markov}'{s}\:{rule} \\ $$$${that}\:{after}\:{enough}\:{random}\:{walks}\:{on}\:{a}\:{graph}, \\ $$$${the}\:{probability}\:{of}\:{being}\:{on}\:{any}\:{vertex}\: \\ $$$${is}\:{proportional}\:{to}\:{the}\:{number}\:{of}\:{edges} \\ $$$${connected}\:{to}\:{the}\:{given}\:{vertex}.\:{In}\:{our} \\ $$$${case}\:{all}\:{verteces}\:{have}\:\mathrm{4}\:{edges}\:{connected} \\ $$$${to}\:{them},\:{and}\:{therefore}\:{the}\:{probability} \\ $$$${is}\:{the}\:{same}\:{for}\:{all}\:\mathrm{6}\:{verteces},\:{i}.{e}.\:{it}'{s} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}. \\ $$$$ \\ $$
Commented by Tawa11 last updated on 25/Jan/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *