Question-165024

Question Number 165024 by cortano1 last updated on 25/Jan/22

Commented by cortano1 last updated on 25/Jan/22

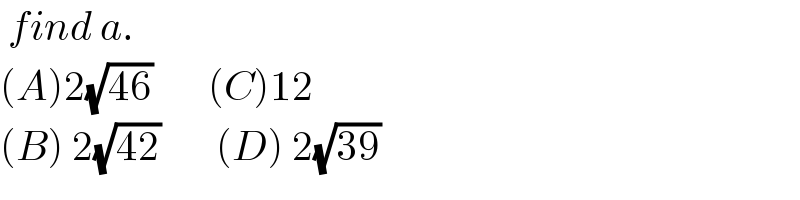
find a. (A)2(√(46)) (C)12 (B) 2(√(42)) (D) 2(√(39))

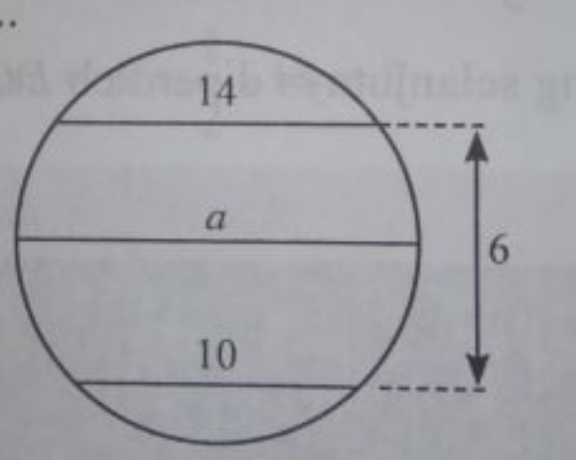
$$\:{find}\:{a}. \\ $$$$\left({A}\right)\mathrm{2}\sqrt{\mathrm{46}}\:\:\:\:\:\:\:\left({C}\right)\mathrm{12} \\ $$$$\left({B}\right)\:\mathrm{2}\sqrt{\mathrm{42}}\:\:\:\:\:\:\:\left({D}\right)\:\mathrm{2}\sqrt{\mathrm{39}} \\ $$

Commented by som(math1967) last updated on 25/Jan/22

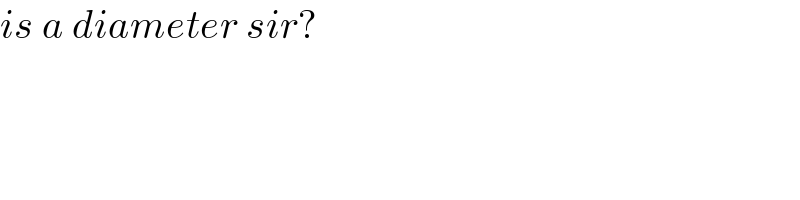
$${is}\:{a}\:{diameter}\:{sir}? \\ $$

Commented by cortano1 last updated on 25/Jan/22

$${no}\:{sir} \\ $$

Commented by mr W last updated on 25/Jan/22

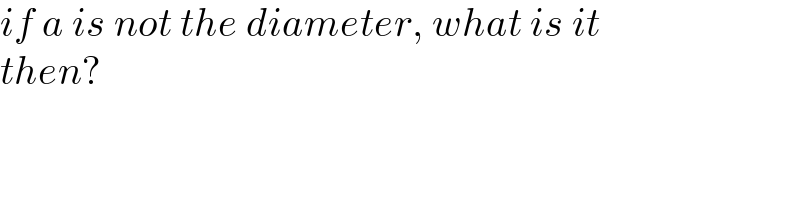
$${if}\:{a}\:{is}\:{not}\:{the}\:{diameter},\:{what}\:{is}\:{it} \\ $$$${then}? \\ $$

Commented by cortano1 last updated on 25/Jan/22

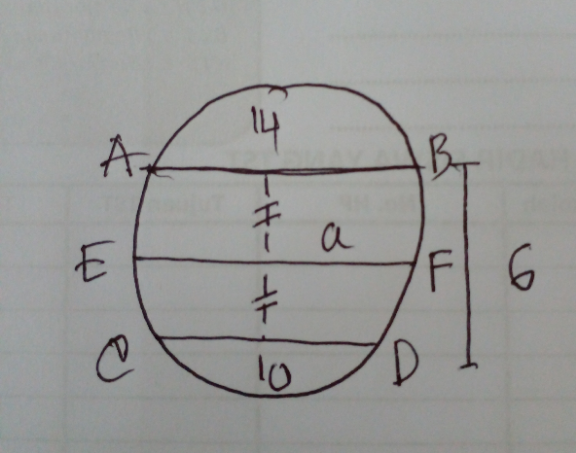
Commented by som(math1967) last updated on 25/Jan/22

$${a}=\mathrm{2}\sqrt{\mathrm{46}}\:? \\ $$

Commented by cortano1 last updated on 25/Jan/22

$${how}\:{sir}? \\ $$

Answered by mr W last updated on 25/Jan/22

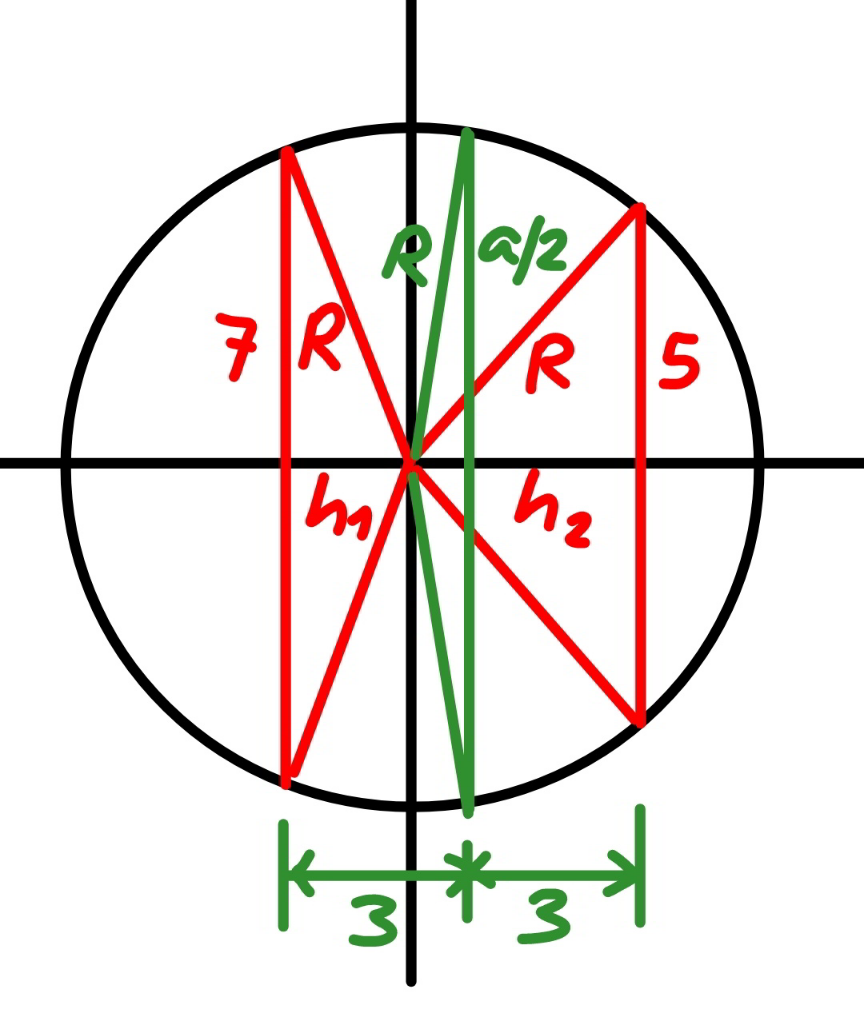
Commented by mr W last updated on 25/Jan/22

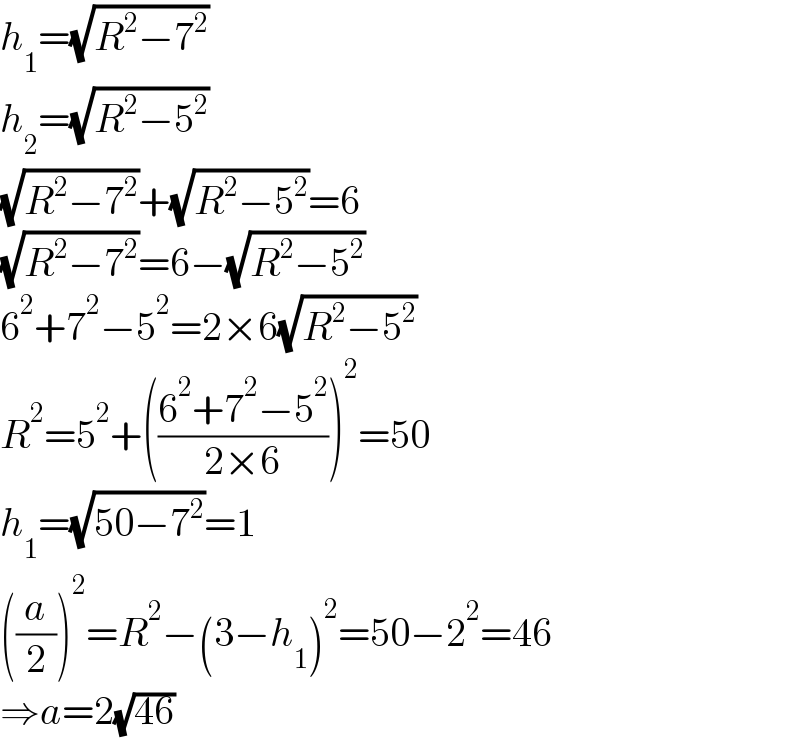
h_1 =(√(R^2 −7^2 )) h_2 =(√(R^2 −5^2 )) (√(R^2 −7^2 ))+(√(R^2 −5^2 ))=6 (√(R^2 −7^2 ))=6−(√(R^2 −5^2 )) 6^2 +7^2 −5^2 =2×6(√(R^2 −5^2 )) R^2 =5^2 +(((6^2 +7^2 −5^2 )/(2×6)))^2 =50 h_1 =(√(50−7^2 ))=1 ((a/2))^2 =R^2 −(3−h_1 )^2 =50−2^2 =46 ⇒a=2(√(46))

$${h}_{\mathrm{1}} =\sqrt{{R}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} } \\ $$$${h}_{\mathrm{2}} =\sqrt{{R}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} } \\ $$$$\sqrt{{R}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }+\sqrt{{R}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }=\mathrm{6} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }=\mathrm{6}−\sqrt{{R}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} } \\ $$$$\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} =\mathrm{2}×\mathrm{6}\sqrt{{R}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\left(\frac{\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }{\mathrm{2}×\mathrm{6}}\right)^{\mathrm{2}} =\mathrm{50} \\ $$$${h}_{\mathrm{1}} =\sqrt{\mathrm{50}−\mathrm{7}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} −\left(\mathrm{3}−{h}_{\mathrm{1}} \right)^{\mathrm{2}} =\mathrm{50}−\mathrm{2}^{\mathrm{2}} =\mathrm{46} \\ $$$$\Rightarrow{a}=\mathrm{2}\sqrt{\mathrm{46}} \\ $$

Commented by Tawa11 last updated on 25/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply