Question Number 165150 by ajfour last updated on 26/Jan/22
Commented by ajfour last updated on 26/Jan/22
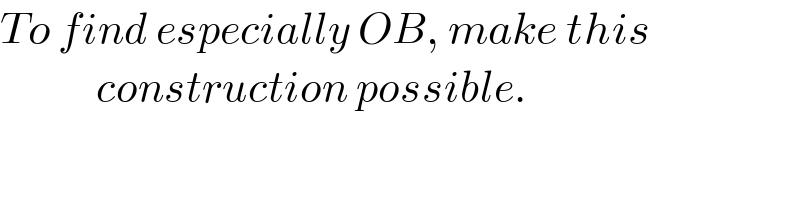
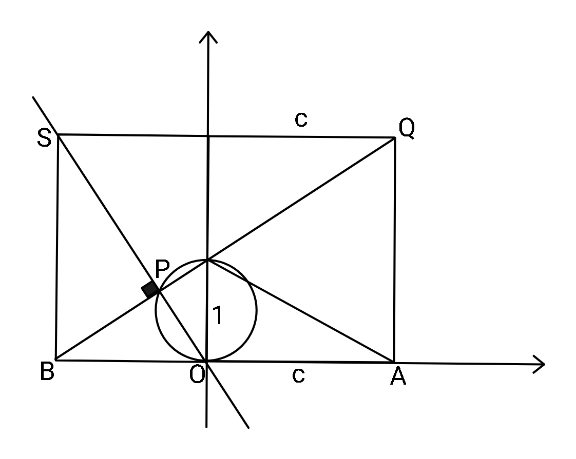
$${To}\:{find}\:{especially}\:{OB},\:{make}\:{this} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{construction}\:{possible}. \\ $$
Answered by aleks041103 last updated on 27/Jan/22

$${N}={l}\cap{BQ},\:{l}\bot{AB},\:{O}\in{l} \\ $$$${let}\:{OB}={a}: \\ $$$$\bigtriangleup{BON}\sim\bigtriangleup{BAQ} \\ $$$$\Rightarrow\frac{{AQ}}{{ON}}={AQ}=\frac{{c}+{a}}{{a}}=\frac{{AB}}{{OB}},\:{where}\:{ON}=\mathrm{1} \\ $$$${AQ}={BS}\Rightarrow{BS}=\mathrm{1}+\frac{{c}}{{a}} \\ $$$$\measuredangle{BPS}=\mathrm{90}°\Rightarrow\frac{{BS}}{{BO}}\:\frac{{ON}}{{OB}}=\mathrm{1} \\ $$$$\frac{{c}+{a}}{{a}^{\mathrm{2}} }=\frac{{a}}{\mathrm{1}}\Rightarrow{a}^{\mathrm{3}} −{a}−{c}=\mathrm{0} \\ $$$$\Rightarrow{For}\:{this}\:{construction}\:{to}\:{be}\:{possible}: \\ $$$${OB}^{\mathrm{3}} −{OB}={c} \\ $$$${or} \\ $$$${OB}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{27}{c}+\mathrm{3}\sqrt{\mathrm{3}}\sqrt{\mathrm{27}{c}^{\mathrm{2}} −\mathrm{4}}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{9}{c}+\sqrt{\mathrm{3}}\sqrt{\mathrm{27}{c}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{18}}} \\ $$
Commented by ajfour last updated on 27/Jan/22
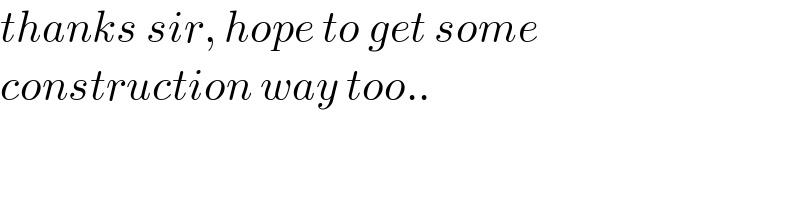
$${thanks}\:{sir},\:{hope}\:{to}\:{get}\:{some} \\ $$$${construction}\:{way}\:{too}.. \\ $$
