Question Number 165183 by mathlove last updated on 27/Jan/22
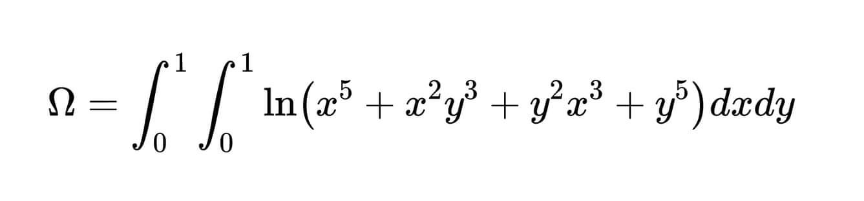
Commented by Ar Brandon last updated on 27/Jan/22
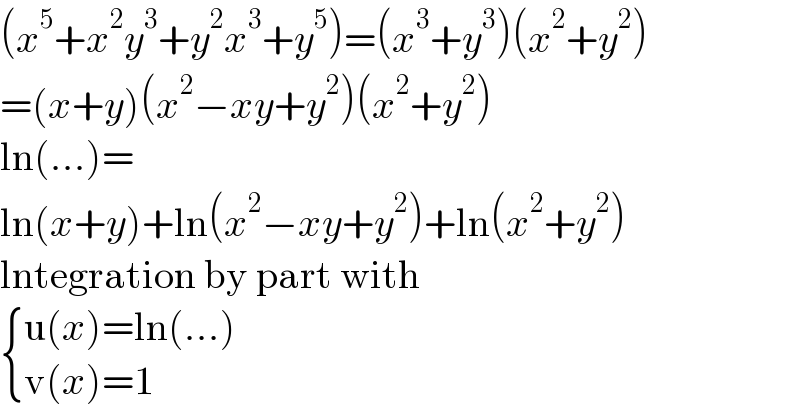
$$\left({x}^{\mathrm{5}} +{x}^{\mathrm{2}} {y}^{\mathrm{3}} +{y}^{\mathrm{2}} {x}^{\mathrm{3}} +{y}^{\mathrm{5}} \right)=\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$=\left({x}+{y}\right)\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\mathrm{ln}\left(…\right)= \\ $$$$\mathrm{ln}\left({x}+{y}\right)+\mathrm{ln}\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)+\mathrm{ln}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\mathrm{lntegration}\:\mathrm{by}\:\mathrm{part}\:\mathrm{with} \\ $$$$\begin{cases}{\mathrm{u}\left({x}\right)=\mathrm{ln}\left(…\right)}\\{\mathrm{v}\left({x}\right)=\mathrm{1}}\end{cases} \\ $$
