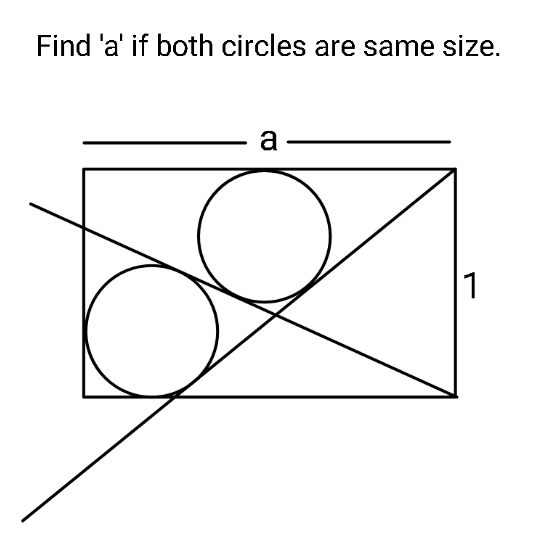
Question Number 165217 by ajfour last updated on 27/Jan/22
Commented by mr W last updated on 28/Jan/22
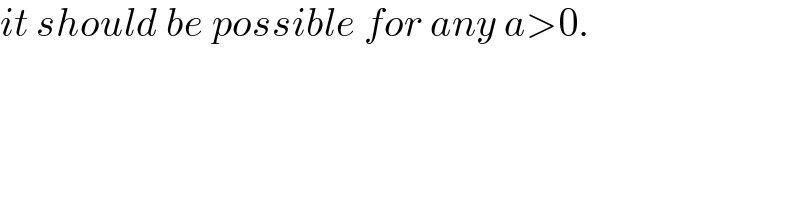
$${it}\:{should}\:{be}\:{possible}\:{for}\:{any}\:{a}>\mathrm{0}. \\ $$
Commented by mr W last updated on 28/Jan/22

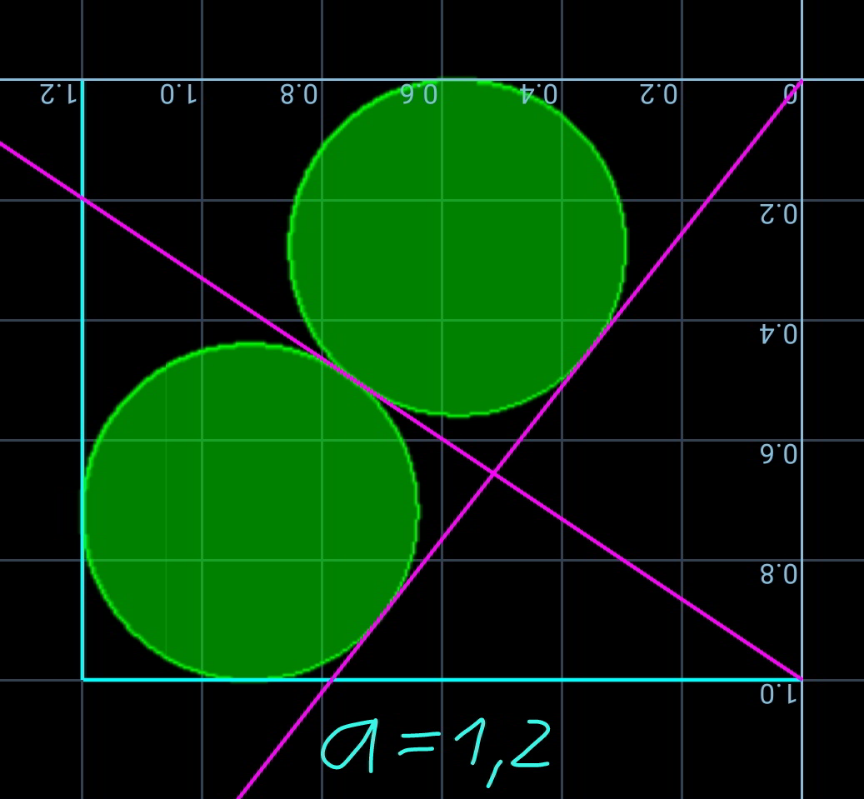
$${nice}\:{question}\:{sir}! \\ $$$${it}\:{seems}\:{to}\:{have}\:{no}\:{unique}\:{solution}. \\ $$$${that}\:{means}\:{it}\:{is}\:{possible}\:{for}\:{a}\:{range} \\ $$$${of}\:{values}\:{of}\:{a},\:{not}\:{a}\:{single}\:{one}. \\ $$
Commented by mr W last updated on 28/Jan/22
Commented by mr W last updated on 28/Jan/22

Commented by ajfour last updated on 28/Jan/22
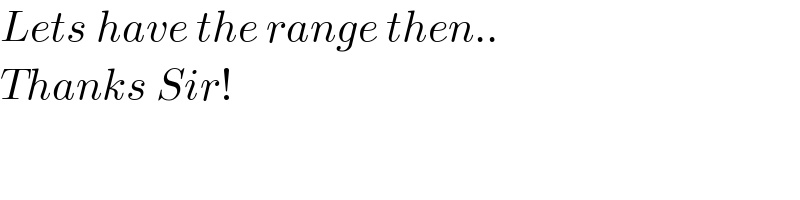
$${Lets}\:{have}\:{the}\:{range}\:{then}.. \\ $$$${Thanks}\:{Sir}! \\ $$
Answered by mr W last updated on 28/Jan/22
Commented by mr W last updated on 28/Jan/22
![we take O as origin. let m=tan θ, k=tan ϕ A(0,1) B(a,0) C_1 (a−r,1−r) C_2 (h,r) eqn. of OE: mx−y=0 eqn. of AD: kx+y−1=0 r(√(m^2 +1))=(a−r)m−(1−r) r(√(m^2 +1))=hm−r (a−r)m−(1−r)=hm−r ⇒h=a−r−((1−2r)/m) ✓ r(√(m^2 +1))=(a−r)m−(1−r) ⇒r=((am−1)/(m+(√(m^2 −1))−1)) ✓ r(√(k^2 +1))=(a−r)k+(1−r)−1 r(√(k^2 +1))=−(hk+r−1) (a−r)k+(1−r)−1=−(hk+r−1) 1−(a−r)k=hk ⇒h=(1/k)−(a−r) ✓ r(√(k^2 +1))=−[1−(a−r)k+r−1] ⇒r=((ak)/( 1+k+(√(k^2 +1)))) ✓ (1/k)−a+r=a−r−((1−2r)/m) (1/k)=2(a−r)−((1−2r)/m) (1/k)=2a−(1/m)+2((1/m)−1)r ⇒k=(1/(2a−(1/m)+2((1/m)−1)r)) ✓ for any given a we can obtain m from ((am−1)/(m+(√(m^2 −1))−1))=((ak)/( 1+k+(√(k^2 +1))))](https://www.tinkutara.com/question/Q165279.png)
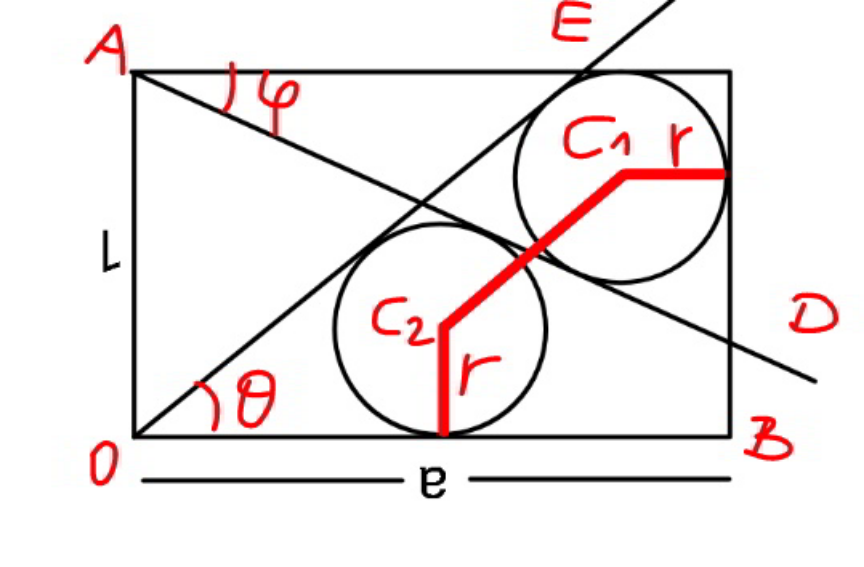
$${we}\:{take}\:{O}\:{as}\:{origin}. \\ $$$${let}\:{m}=\mathrm{tan}\:\theta,\:{k}=\mathrm{tan}\:\varphi \\ $$$${A}\left(\mathrm{0},\mathrm{1}\right) \\ $$$${B}\left({a},\mathrm{0}\right) \\ $$$${C}_{\mathrm{1}} \left({a}−{r},\mathrm{1}−{r}\right) \\ $$$${C}_{\mathrm{2}} \left({h},{r}\right) \\ $$$${eqn}.\:{of}\:{OE}: \\ $$$${mx}−{y}=\mathrm{0} \\ $$$${eqn}.\:{of}\:{AD}: \\ $$$${kx}+{y}−\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$${r}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}=\left({a}−{r}\right){m}−\left(\mathrm{1}−{r}\right) \\ $$$${r}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}={hm}−{r} \\ $$$$\left({a}−{r}\right){m}−\left(\mathrm{1}−{r}\right)={hm}−{r} \\ $$$$\Rightarrow{h}={a}−{r}−\frac{\mathrm{1}−\mathrm{2}{r}}{{m}}\:\checkmark \\ $$$${r}\sqrt{{m}^{\mathrm{2}} +\mathrm{1}}=\left({a}−{r}\right){m}−\left(\mathrm{1}−{r}\right) \\ $$$$\Rightarrow{r}=\frac{{am}−\mathrm{1}}{{m}+\sqrt{{m}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}}\:\checkmark \\ $$$$ \\ $$$${r}\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=\left({a}−{r}\right){k}+\left(\mathrm{1}−{r}\right)−\mathrm{1} \\ $$$${r}\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=−\left({hk}+{r}−\mathrm{1}\right) \\ $$$$\left({a}−{r}\right){k}+\left(\mathrm{1}−{r}\right)−\mathrm{1}=−\left({hk}+{r}−\mathrm{1}\right) \\ $$$$\mathrm{1}−\left({a}−{r}\right){k}={hk} \\ $$$$\Rightarrow{h}=\frac{\mathrm{1}}{{k}}−\left({a}−{r}\right)\:\checkmark \\ $$$${r}\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=−\left[\mathrm{1}−\left({a}−{r}\right){k}+{r}−\mathrm{1}\right] \\ $$$$\Rightarrow{r}=\frac{{ak}}{\:\mathrm{1}+{k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}\:\checkmark \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{k}}−{a}+{r}={a}−{r}−\frac{\mathrm{1}−\mathrm{2}{r}}{{m}} \\ $$$$\frac{\mathrm{1}}{{k}}=\mathrm{2}\left({a}−{r}\right)−\frac{\mathrm{1}−\mathrm{2}{r}}{{m}} \\ $$$$\frac{\mathrm{1}}{{k}}=\mathrm{2}{a}−\frac{\mathrm{1}}{{m}}+\mathrm{2}\left(\frac{\mathrm{1}}{{m}}−\mathrm{1}\right){r} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{2}{a}−\frac{\mathrm{1}}{{m}}+\mathrm{2}\left(\frac{\mathrm{1}}{{m}}−\mathrm{1}\right){r}}\:\checkmark \\ $$$$ \\ $$$${for}\:{any}\:{given}\:{a}\:{we}\:{can}\:{obtain}\:{m}\:{from} \\ $$$$\frac{{am}−\mathrm{1}}{{m}+\sqrt{{m}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}}=\frac{{ak}}{\:\mathrm{1}+{k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}}\: \\ $$
Commented by mr W last updated on 28/Jan/22

Commented by mr W last updated on 28/Jan/22
Commented by mr W last updated on 28/Jan/22

Commented by ajfour last updated on 28/Jan/22
$${Thanks}\:{sir},\:{i}\:{will}\:{go}\:{through}.. \\ $$
Commented by Tawa11 last updated on 28/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 28/Jan/22
Commented by ajfour last updated on 28/Jan/22
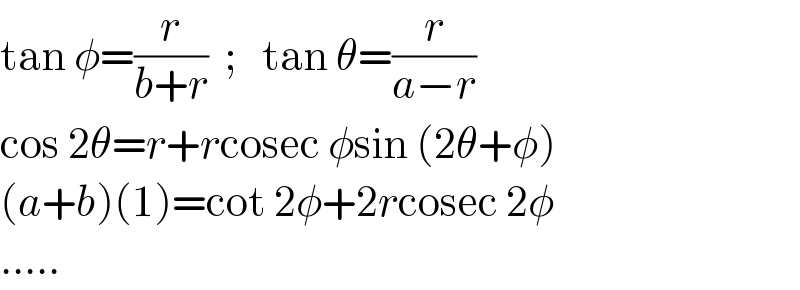
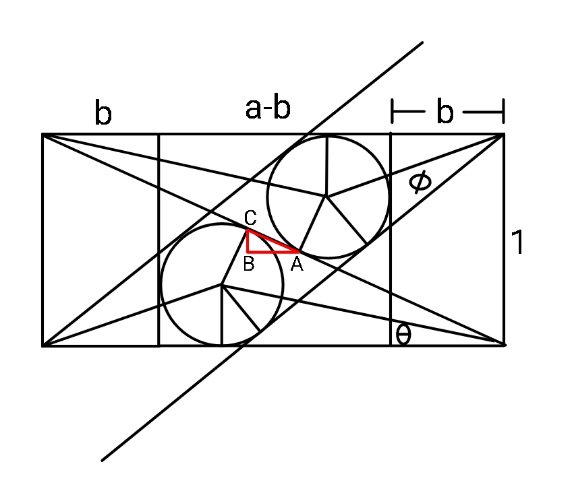
$$\mathrm{tan}\:\phi=\frac{{r}}{{b}+{r}}\:\:;\:\:\:\mathrm{tan}\:\theta=\frac{{r}}{{a}−{r}} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta={r}+{r}\mathrm{cosec}\:\phi\mathrm{sin}\:\left(\mathrm{2}\theta+\phi\right) \\ $$$$\left({a}+{b}\right)\left(\mathrm{1}\right)=\mathrm{cot}\:\mathrm{2}\phi+\mathrm{2}{r}\mathrm{cosec}\:\mathrm{2}\phi \\ $$$$….. \\ $$
