Question Number 165232 by Neils last updated on 27/Jan/22
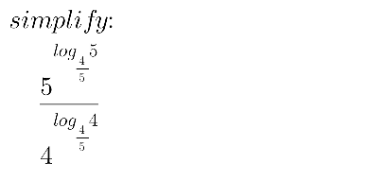
Commented by bobhans last updated on 30/Jan/22

Answered by FelipeLz last updated on 27/Jan/22
![5^(log_(4/5) (5)) = e^(ln(5)log_(4/5) (5)) = e^((ln^2 (5))/(ln(4)−ln(5))) 4^(log_(4/5) (4)) = e^(ln(4)log_(4/5) (4)) = e^((ln^2 (4))/(ln(4)−ln(5))) (e^((ln^2 (5))/(ln(4)−ln(5))) /e^((ln^2 (4))/(ln(4)−ln(5))) ) = e^((ln^2 (5)−ln^2 (4))/(ln(4)−ln(5))) = e^((−[ln(4)−ln(5)][ln(4)+ln(5)])/(ln(4)−ln(5))) = e^(−[ln(4)+ln(5)]) = e^(−ln(20)) = (1/(20))](https://www.tinkutara.com/question/Q165237.png)
$$\mathrm{5}^{\mathrm{log}_{\frac{\mathrm{4}}{\mathrm{5}}} \left(\mathrm{5}\right)} \:=\:{e}^{\mathrm{ln}\left(\mathrm{5}\right)\mathrm{log}_{\frac{\mathrm{4}}{\mathrm{5}}} \left(\mathrm{5}\right)} \:=\:{e}^{\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{5}\right)}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)}} \\ $$$$\mathrm{4}^{\mathrm{log}_{\frac{\mathrm{4}}{\mathrm{5}}} \left(\mathrm{4}\right)} \:=\:{e}^{\mathrm{ln}\left(\mathrm{4}\right)\mathrm{log}_{\frac{\mathrm{4}}{\mathrm{5}}} \left(\mathrm{4}\right)} \:=\:{e}^{\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{4}\right)}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)}} \\ $$$$\frac{{e}^{\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{5}\right)}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)}} }{{e}^{\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{4}\right)}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)}} }\:=\:{e}^{\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{5}\right)−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{4}\right)}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)}} \:=\:{e}^{\frac{−\left[\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)\right]\left[\mathrm{ln}\left(\mathrm{4}\right)+\mathrm{ln}\left(\mathrm{5}\right)\right]}{\mathrm{ln}\left(\mathrm{4}\right)−\mathrm{ln}\left(\mathrm{5}\right)}} =\:{e}^{−\left[\mathrm{ln}\left(\mathrm{4}\right)+\mathrm{ln}\left(\mathrm{5}\right)\right]} \:=\:{e}^{−\mathrm{ln}\left(\mathrm{20}\right)} \:=\:\frac{\mathrm{1}}{\mathrm{20}} \\ $$
Commented by Neils last updated on 27/Jan/22

$${Nice}\:{Solution} \\ $$
