Menu Close

Question-165270

Tinku Tara 0 Comments
Pin




Question Number 165270 by cortano1 last updated on 28/Jan/22
Answered by TheSupreme last updated on 28/Jan/22
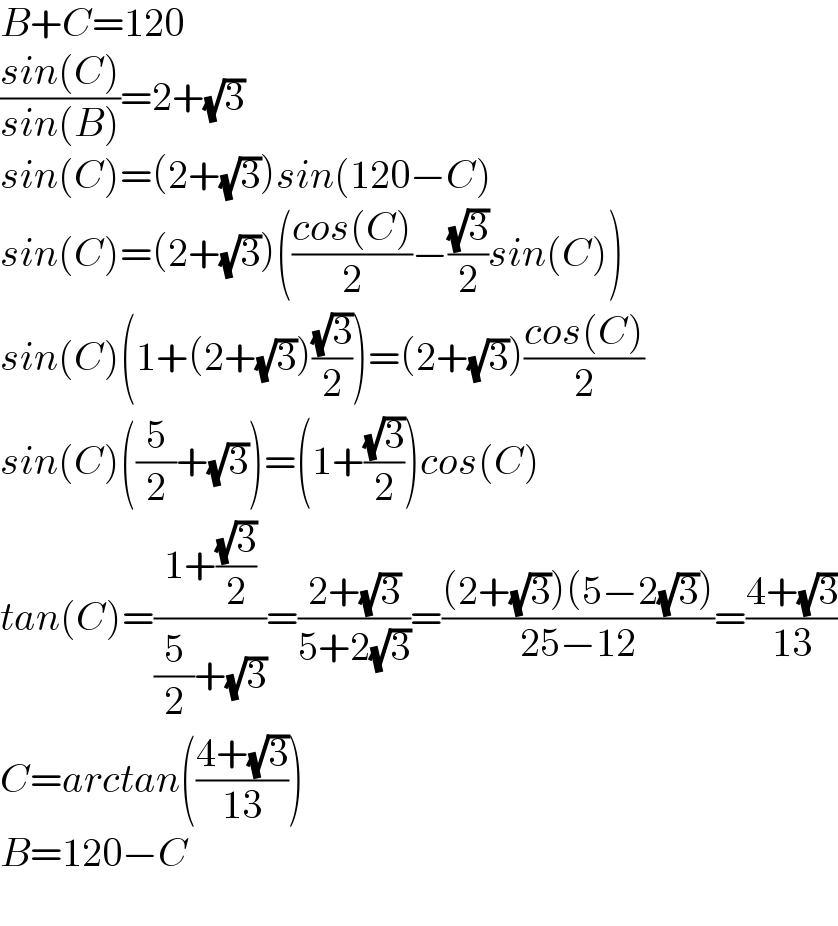
B+C=120 ((sin(C))/(sin(B)))=2+(√3) sin(C)=(2+(√3))sin(120−C) sin(C)=(2+(√3))(((cos(C))/2)−((√3)/2)sin(C)) sin(C)(1+(2+(√3))((√3)/2))=(2+(√3))((cos(C))/2) sin(C)((5/2)+(√3))=(1+((√3)/2))cos(C) tan(C)=((1+((√3)/2))/((5/2)+(√3)))=((2+(√3))/(5+2(√3)))=(((2+(√3))(5−2(√3)))/(25−12))=((4+(√3))/(13)) C=arctan(((4+(√3))/(13))) B=120−C
$${B}+{C}=\mathrm{120} \\ $$$$\frac{{sin}\left({C}\right)}{{sin}\left({B}\right)}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${sin}\left({C}\right)=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){sin}\left(\mathrm{120}−{C}\right) \\ $$$${sin}\left({C}\right)=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\frac{{cos}\left({C}\right)}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\left({C}\right)\right) \\ $$$${sin}\left({C}\right)\left(\mathrm{1}+\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\frac{{cos}\left({C}\right)}{\mathrm{2}} \\ $$$${sin}\left({C}\right)\left(\frac{\mathrm{5}}{\mathrm{2}}+\sqrt{\mathrm{3}}\right)=\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right){cos}\left({C}\right) \\ $$$${tan}\left({C}\right)=\frac{\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{\mathrm{5}}{\mathrm{2}}+\sqrt{\mathrm{3}}}=\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{3}}\right)}{\mathrm{25}−\mathrm{12}}=\frac{\mathrm{4}+\sqrt{\mathrm{3}}}{\mathrm{13}} \\ $$$${C}={arctan}\left(\frac{\mathrm{4}+\sqrt{\mathrm{3}}}{\mathrm{13}}\right) \\ $$$${B}=\mathrm{120}−{C} \\ $$$$ \\ $$
Answered by mr W last updated on 28/Jan/22
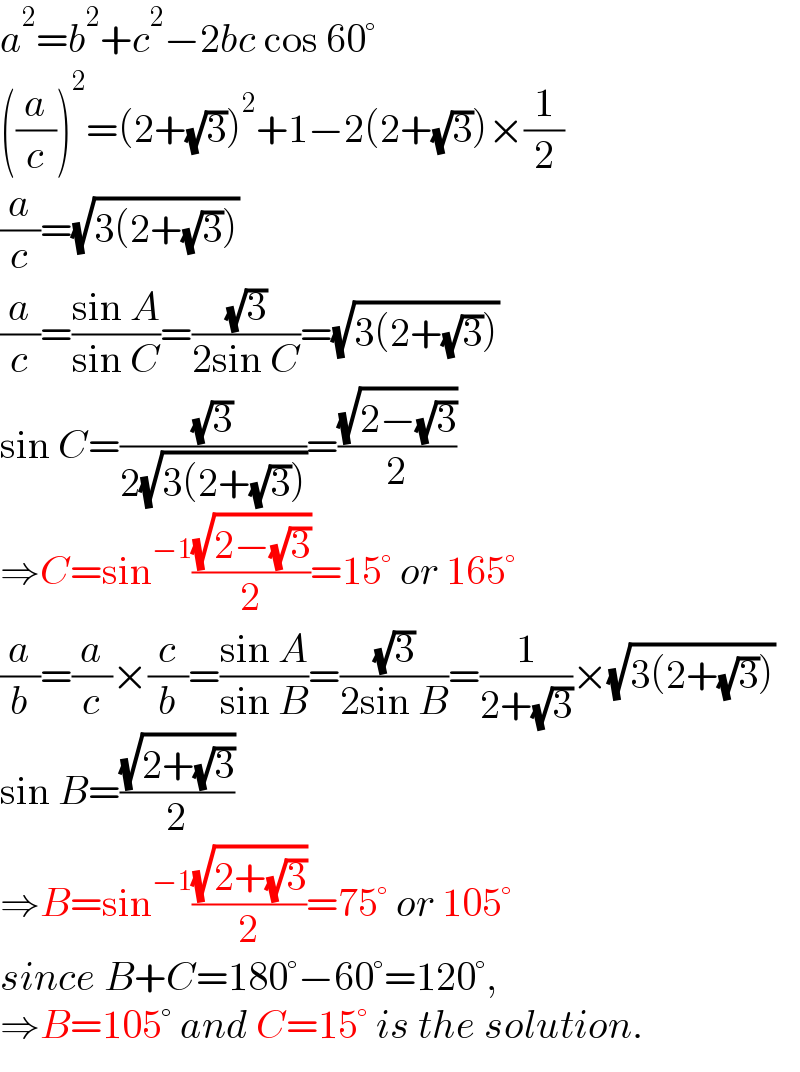
a^2 =b^2 +c^2 −2bc cos 60° ((a/c))^2 =(2+(√3))^2 +1−2(2+(√3))×(1/2) (a/c)=(√(3(2+(√3)))) (a/c)=((sin A)/(sin C))=((√3)/(2sin C))=(√(3(2+(√3)))) sin C=((√3)/(2(√(3(2+(√3))))))=((√(2−(√3)))/2) ⇒C=sin^(−1) ((√(2−(√3)))/2)=15° or 165° (a/b)=(a/c)×(c/b)=((sin A)/(sin B))=((√3)/(2sin B))=(1/(2+(√3)))×(√(3(2+(√3)))) sin B=((√(2+(√3)))/2) ⇒B=sin^(−1) ((√(2+(√3)))/2)=75° or 105° since B+C=180°−60°=120°, ⇒B=105° and C=15° is the solution.
$${a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:\mathrm{60}° \\ $$$$\left(\frac{{a}}{{c}}\right)^{\mathrm{2}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{a}}{{c}}=\sqrt{\mathrm{3}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$$\frac{{a}}{{c}}=\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{C}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2sin}\:{C}}=\sqrt{\mathrm{3}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$$\mathrm{sin}\:{C}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{3}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}}=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$\Rightarrow{C}=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}=\mathrm{15}°\:{or}\:\mathrm{165}° \\ $$$$\frac{{a}}{{b}}=\frac{{a}}{{c}}×\frac{{c}}{{b}}=\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{B}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2sin}\:{B}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}×\sqrt{\mathrm{3}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)} \\ $$$$\mathrm{sin}\:{B}=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$\Rightarrow{B}=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}}=\mathrm{75}°\:{or}\:\mathrm{105}° \\ $$$${since}\:{B}+{C}=\mathrm{180}°−\mathrm{60}°=\mathrm{120}°, \\ $$$$\Rightarrow{B}=\mathrm{105}°\:{and}\:{C}=\mathrm{15}°\:{is}\:{the}\:{solution}. \\ $$
Commented by mr W last updated on 29/Jan/22
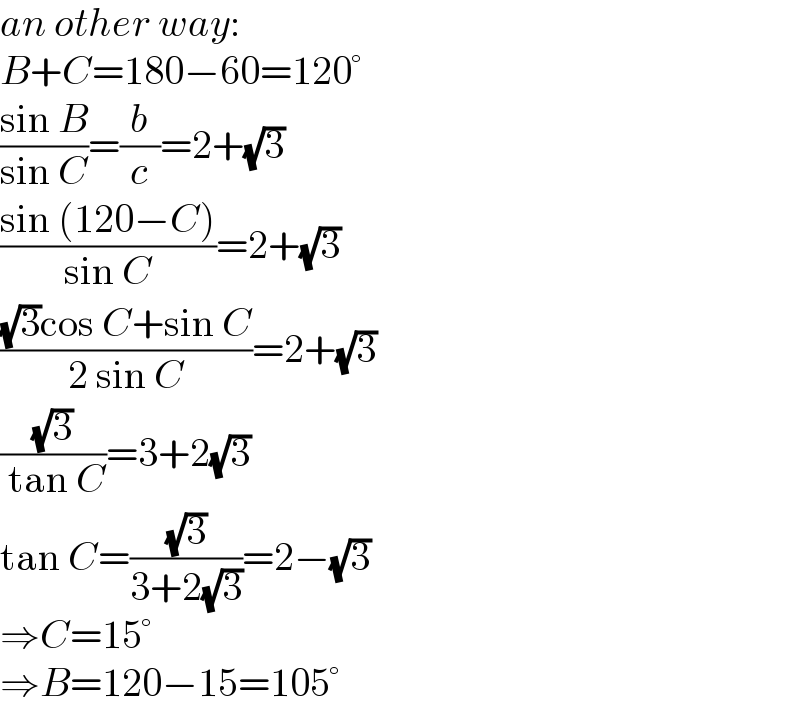
an other way: B+C=180−60=120° ((sin B)/(sin C))=(b/c)=2+(√3) ((sin (120−C))/(sin C))=2+(√3) (((√3)cos C+sin C)/(2 sin C))=2+(√3) ((√3)/( tan C))=3+2(√3) tan C=((√3)/(3+2(√3)))=2−(√3) ⇒C=15° ⇒B=120−15=105°
$${an}\:{other}\:{way}: \\ $$$${B}+{C}=\mathrm{180}−\mathrm{60}=\mathrm{120}° \\ $$$$\frac{\mathrm{sin}\:{B}}{\mathrm{sin}\:{C}}=\frac{{b}}{{c}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{120}−{C}\right)}{\mathrm{sin}\:{C}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\frac{\sqrt{\mathrm{3}}\mathrm{cos}\:{C}+\mathrm{sin}\:{C}}{\mathrm{2}\:\mathrm{sin}\:{C}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\:\mathrm{tan}\:{C}}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{tan}\:{C}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{C}=\mathrm{15}° \\ $$$$\Rightarrow{B}=\mathrm{120}−\mathrm{15}=\mathrm{105}° \\ $$
Commented by cortano1 last updated on 29/Jan/22
nice
$${nice} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *