Question Number 165291 by HongKing last updated on 28/Jan/22

Answered by mahdipoor last updated on 29/Jan/22
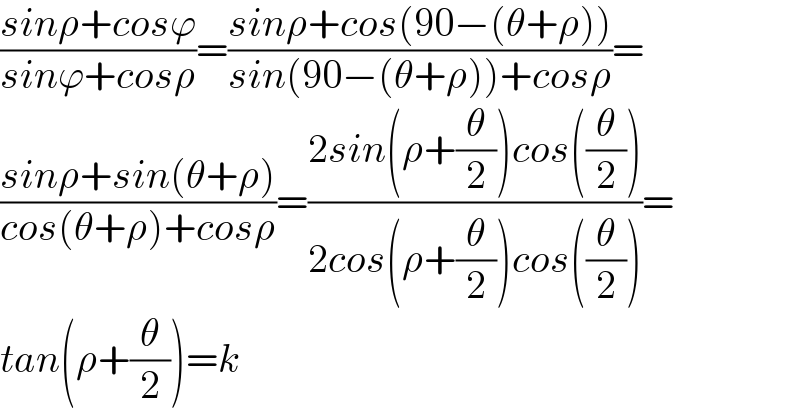
$$\frac{{sin}\rho+{cos}\varphi}{{sin}\varphi+{cos}\rho}=\frac{{sin}\rho+{cos}\left(\mathrm{90}−\left(\theta+\rho\right)\right)}{{sin}\left(\mathrm{90}−\left(\theta+\rho\right)\right)+{cos}\rho}= \\ $$$$\frac{{sin}\rho+{sin}\left(\theta+\rho\right)}{{cos}\left(\theta+\rho\right)+{cos}\rho}=\frac{\mathrm{2}{sin}\left(\rho+\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2}{cos}\left(\rho+\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right)}= \\ $$$${tan}\left(\rho+\frac{\theta}{\mathrm{2}}\right)={k} \\ $$
Commented by HongKing last updated on 01/Feb/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
