Menu Close

Question-165357

Tinku Tara 0 Comments
Pin




Question Number 165357 by ajfour last updated on 31/Jan/22
Commented by ajfour last updated on 31/Jan/22
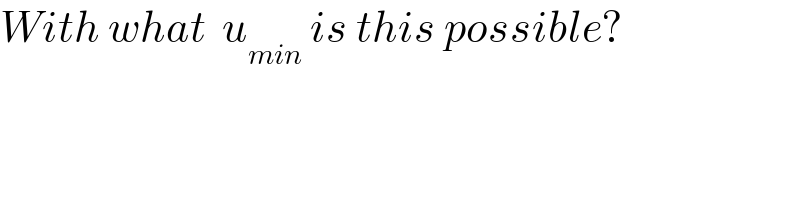
With what u_(min) is this possible?
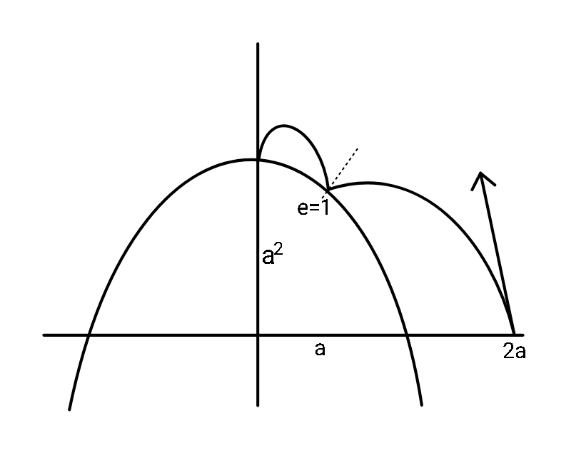
$${With}\:{what}\:\:{u}_{{min}} \:{is}\:{this}\:{possible}? \\ $$
Commented by ajfour last updated on 01/Feb/22
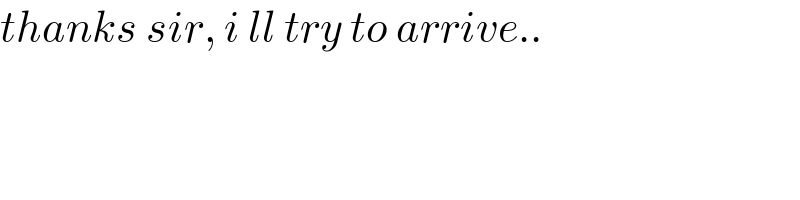
thanks sir, i ll try to arrive..
$${thanks}\:{sir},\:{i}\:{ll}\:{try}\:{to}\:{arrive}.. \\ $$
Answered by ajfour last updated on 01/Feb/22
Parabola: y=a^2 −x^2 let at firsr collision point P (b, a^2 −b^2 ) (dy/dx)=−2x=−2b=−tan θ ⇒ tan θ=2b t_1 =((2a−b)/u_x ) a^2 −b^2 =u_y t_1 −((gt_1 ^2 )/2) ⇒ a^2 −b^2 =(2a−b)tan φ−((g(2a−b)^2 (1+tan^2 φ))/(2u^2 )) let just before reaching P v_x =u_x , v_y =u_y −gt_1 ⇒ tan φ=(((a^2 −b^2 )/(2a−b)))+((g(2a−b)(1+tan^2 φ))/(2u^2 )) ....(ii) or ((2u^2 )/(g(1+4b^2 )))=((2a−b)/((tan φ−((a^2 −b^2 )/(2a−b))))) ..(I) ⇒ (v_y /v_x )=tan φ=A+(B/u_x ^2 ) ...(i) & now due to reflection of velocity, let just after hitting P, velocity be V. V_x cos θ+V_y sin θ=u_x cos θ+v_y sin θ & V_y cos θ−V_x sin θ=u_x sin θ−v_y cos θ ⇒ V_x +2bV_y =u_x +2bv_y & V_y −2bV_x =2bu_x −v_y ⇒ V_y =((4bu_x +(4b^2 −1)v_y )/(4b^2 +1)) V_x =((4bv_y −(4b^2 −1)u_x )/(4b^2 +1)) t_2 =(b/V_x ) & b^2 =V_y t_2 −((gt_2 ^2 )/2) ⇒ b^2 =b((V_y /V_x ))−(g/2)((b/V_x ))^2 ⇒ b^2 {((4bv_y −(4b^2 −1)u_x )/(4b^2 +1))}^2 =b{((4bv_y −(4b^2 −1)u_x )/(4b^2 +1))}{((4bu_x +(4b^2 −1)v_y )/(4b^2 +1))} −((b^2 g)/2) using ..(i) & u_x =ucos φ, u_y =usin φ b^2 {((4btan φ−(4b^2 −1))/(4b^2 +1))}^2 =b{((4btan φ−(4b^2 −1))/(4b^2 +1))}{((4b+(4b^2 −1)tan φ)/(4b^2 +1))} −((b^2 g(1+tan^2 φ))/(2u^2 )) ....(iii) u can be obtained in terms of tan φ. by the way, i think for u_(min) V_y =gt_2 = ((4bu_x +(4b^2 −1)v_y )/(4b^2 +1)) ⇒ ((bg)/({((4bv_y −(4b^2 −1)u_x )/(4b^2 +1))}))=((4bu_x +(4b^2 −1)v_y )/(4b^2 +1)) ⇒ bg(4b^2 +1)^2 =u^2 {4btan φ−(4b^2 −1)}{4b+(4b^2 −1)tan φ} & ((2u^2 )/((1+4b^2 )g))=((2a−b)/((tan φ−((a^2 −b^2 )/(2a−b))))) ⇒ ((2b(1+4b^2 )(tan φ−((a^2 −b^2 )/(2a−b))))/(2a−b)) ={4btan φ−(4b^2 −1)}{4b+(4b^2 −1)tan φ} ....hopeless....
$${Parabola}:\:\:{y}={a}^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$${let}\:{at}\:{firsr}\:{collision}\:{point}\: \\ $$$${P}\:\left({b},\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=−\mathrm{2}{x}=−\mathrm{2}{b}=−\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta=\mathrm{2}{b} \\ $$$${t}_{\mathrm{1}} =\frac{\mathrm{2}{a}−{b}}{{u}_{{x}} } \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={u}_{{y}} {t}_{\mathrm{1}} −\frac{{gt}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left(\mathrm{2}{a}−{b}\right)\mathrm{tan}\:\phi−\frac{{g}\left(\mathrm{2}{a}−{b}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \phi\right)}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${let}\:{just}\:{before}\:{reaching}\:{P} \\ $$$${v}_{{x}} ={u}_{{x}} \:,\:{v}_{{y}} ={u}_{{y}} −{gt}_{\mathrm{1}} \:\:\:\Rightarrow \\ $$$$\mathrm{tan}\:\phi=\left(\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{a}−{b}}\right)+\frac{{g}\left(\mathrm{2}{a}−{b}\right)\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \phi\right)}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:….\left({ii}\right) \\ $$$${or}\:\:\:\frac{\mathrm{2}{u}^{\mathrm{2}} }{{g}\left(\mathrm{1}+\mathrm{4}{b}^{\mathrm{2}} \right)}=\frac{\mathrm{2}{a}−{b}}{\left(\mathrm{tan}\:\phi−\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{a}−{b}}\right)}\:\:..\left({I}\right) \\ $$$$\Rightarrow\:\:\frac{{v}_{{y}} }{{v}_{{x}} }=\mathrm{tan}\:\phi={A}+\frac{{B}}{{u}_{{x}} ^{\mathrm{2}} }\:\:\:…\left({i}\right) \\ $$$$\&\:\: \\ $$$${now}\:{due}\:{to}\:{reflection}\:{of}\:{velocity}, \\ $$$$\:\:{let}\:{just}\:{after}\:{hitting}\:{P}, \\ $$$${velocity}\:{be}\:{V}. \\ $$$$\:\:{V}_{{x}} \mathrm{cos}\:\theta+{V}_{{y}} \mathrm{sin}\:\theta={u}_{{x}} \mathrm{cos}\:\theta+{v}_{{y}} \mathrm{sin}\:\theta \\ $$$$\&\: \\ $$$$\:\:\:{V}_{{y}} \mathrm{cos}\:\theta−{V}_{{x}} \mathrm{sin}\:\theta={u}_{{x}} \mathrm{sin}\:\theta−{v}_{{y}} \mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{V}_{{x}} +\mathrm{2}{bV}_{{y}} ={u}_{{x}} +\mathrm{2}{bv}_{{y}} \:\:\& \\ $$$$\:\:\:\:\:\:\:\:{V}_{{y}} −\mathrm{2}{bV}_{{x}} =\mathrm{2}{bu}_{{x}} −{v}_{{y}} \\ $$$$\Rightarrow\:\:{V}_{{y}} =\frac{\mathrm{4}{bu}_{{x}} +\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){v}_{{y}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:{V}_{{x}} =\frac{\mathrm{4}{bv}_{{y}} −\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){u}_{{x}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$${t}_{\mathrm{2}} =\frac{{b}}{{V}_{{x}} }\:\:\&\:\:\:{b}^{\mathrm{2}} ={V}_{{y}} {t}_{\mathrm{2}} −\frac{{gt}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} ={b}\left(\frac{{V}_{{y}} }{{V}_{{x}} }\right)−\frac{{g}}{\mathrm{2}}\left(\frac{{b}}{{V}_{{x}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} \left\{\frac{\mathrm{4}{bv}_{{y}} −\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){u}_{{x}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\}^{\mathrm{2}} \\ $$$$\:\:={b}\left\{\frac{\mathrm{4}{bv}_{{y}} −\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){u}_{{x}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\}\left\{\frac{\mathrm{4}{bu}_{{x}} +\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){v}_{{y}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\} \\ $$$$\:\:\:\:\:\:\:−\frac{{b}^{\mathrm{2}} {g}}{\mathrm{2}} \\ $$$${using}\:..\left({i}\right)\:\&\:{u}_{{x}} ={u}\mathrm{cos}\:\phi,\:{u}_{{y}} ={u}\mathrm{sin}\:\phi \\ $$$${b}^{\mathrm{2}} \left\{\frac{\mathrm{4}{b}\mathrm{tan}\:\phi−\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\}^{\mathrm{2}} \\ $$$$={b}\left\{\frac{\mathrm{4}{b}\mathrm{tan}\:\phi−\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\}\left\{\frac{\mathrm{4}{b}+\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}\:\phi}{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{b}^{\mathrm{2}} {g}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \phi\right)}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\:\:….\left({iii}\right) \\ $$$${u}\:{can}\:{be}\:{obtained}\:{in}\:{terms}\:{of} \\ $$$$\:\:\mathrm{tan}\:\phi. \\ $$$${by}\:{the}\:{way},\:{i}\:{think}\:{for}\:{u}_{{min}} \\ $$$$\:\:\:{V}_{{y}} ={gt}_{\mathrm{2}} \:\:=\:\:\frac{\mathrm{4}{bu}_{{x}} +\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){v}_{{y}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\:\:\frac{{bg}}{\left\{\frac{\mathrm{4}{bv}_{{y}} −\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){u}_{{x}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}}\right\}}=\frac{\mathrm{4}{bu}_{{x}} +\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right){v}_{{y}} }{\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\:{bg}\left(\mathrm{4}{b}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} ={u}^{\mathrm{2}} \left\{\mathrm{4}{b}\mathrm{tan}\:\phi−\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)\right\}\left\{\mathrm{4}{b}+\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}\:\phi\right\} \\ $$$$\&\:\:\frac{\mathrm{2}{u}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{4}{b}^{\mathrm{2}} \right){g}}=\frac{\mathrm{2}{a}−{b}}{\left(\mathrm{tan}\:\phi−\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{a}−{b}}\right)} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{b}\left(\mathrm{1}+\mathrm{4}{b}^{\mathrm{2}} \right)\left(\mathrm{tan}\:\phi−\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{a}−{b}}\right)}{\mathrm{2}{a}−{b}} \\ $$$$\:\:=\left\{\mathrm{4}{b}\mathrm{tan}\:\phi−\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)\right\}\left\{\mathrm{4}{b}+\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}\:\phi\right\} \\ $$$$ \\ $$$$….{hopeless}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *