Question Number 165362 by HongKing last updated on 31/Jan/22

Answered by aleks041103 last updated on 01/Feb/22
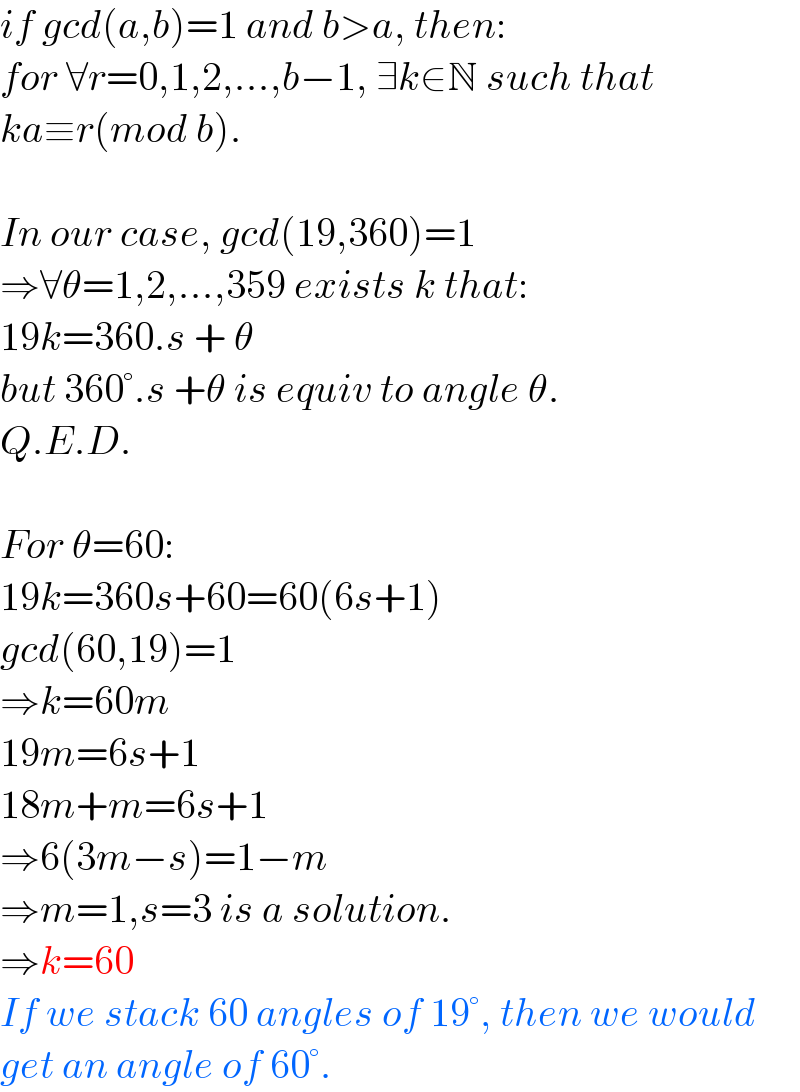
$${if}\:{gcd}\left({a},{b}\right)=\mathrm{1}\:{and}\:{b}>{a},\:{then}: \\ $$$${for}\:\forall{r}=\mathrm{0},\mathrm{1},\mathrm{2},…,{b}−\mathrm{1},\:\exists{k}\in\mathbb{N}\:{such}\:{that} \\ $$$${ka}\equiv{r}\left({mod}\:{b}\right). \\ $$$$ \\ $$$${In}\:{our}\:{case},\:{gcd}\left(\mathrm{19},\mathrm{360}\right)=\mathrm{1} \\ $$$$\Rightarrow\forall\theta=\mathrm{1},\mathrm{2},…,\mathrm{359}\:{exists}\:{k}\:{that}: \\ $$$$\mathrm{19}{k}=\mathrm{360}.{s}\:+\:\theta \\ $$$${but}\:\mathrm{360}°.{s}\:+\theta\:{is}\:{equiv}\:{to}\:{angle}\:\theta. \\ $$$${Q}.{E}.{D}. \\ $$$$ \\ $$$${For}\:\theta=\mathrm{60}: \\ $$$$\mathrm{19}{k}=\mathrm{360}{s}+\mathrm{60}=\mathrm{60}\left(\mathrm{6}{s}+\mathrm{1}\right) \\ $$$${gcd}\left(\mathrm{60},\mathrm{19}\right)=\mathrm{1} \\ $$$$\Rightarrow{k}=\mathrm{60}{m} \\ $$$$\mathrm{19}{m}=\mathrm{6}{s}+\mathrm{1} \\ $$$$\mathrm{18}{m}+{m}=\mathrm{6}{s}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{6}\left(\mathrm{3}{m}−{s}\right)=\mathrm{1}−{m} \\ $$$$\Rightarrow{m}=\mathrm{1},{s}=\mathrm{3}\:{is}\:{a}\:{solution}. \\ $$$$\Rightarrow{k}=\mathrm{60} \\ $$$${If}\:{we}\:{stack}\:\mathrm{60}\:{angles}\:{of}\:\mathrm{19}°,\:{then}\:{we}\:{would} \\ $$$${get}\:{an}\:{angle}\:{of}\:\mathrm{60}°. \\ $$
Commented by HongKing last updated on 01/Feb/22
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
