Question Number 165364 by mathlove last updated on 31/Jan/22

Answered by Ar Brandon last updated on 31/Jan/22

$${S}=\frac{\mathrm{1}}{\mathrm{1}+{e}^{−\mathrm{99}} }+\frac{\mathrm{1}}{\mathrm{1}+{e}^{−\mathrm{98}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{1}+{e}^{\mathrm{98}} }+\frac{\mathrm{1}}{\mathrm{1}+{e}^{\mathrm{99}} } \\ $$$$\:\:\:\:=\frac{{e}^{\mathrm{99}} }{\mathrm{1}+{e}^{\mathrm{99}} }+\frac{{e}^{\mathrm{98}} }{\mathrm{1}+{e}^{\mathrm{98}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{2}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{1}+{e}^{\mathrm{98}} }+\frac{\mathrm{1}}{\mathrm{1}+{e}^{\mathrm{99}} } \\ $$$$\:\:\:\:=\frac{\mathrm{1}+{e}^{\mathrm{99}} }{\mathrm{1}+{e}^{\mathrm{99}} }+\frac{\mathrm{1}+{e}^{\mathrm{98}} }{\mathrm{1}+{e}^{\mathrm{98}} }+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{99}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{199}}{\mathrm{2}} \\ $$
Commented by mathlove last updated on 31/Jan/22

$${thanks} \\ $$
Answered by Ar Brandon last updated on 31/Jan/22
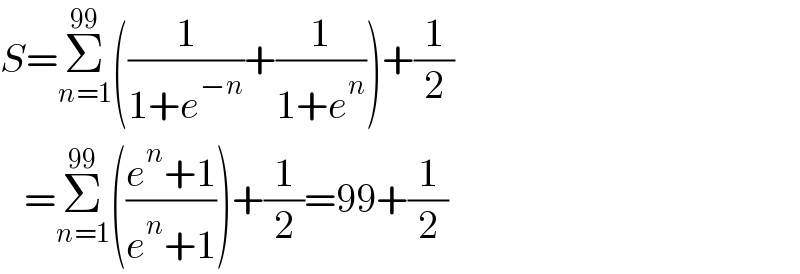
$${S}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{1}+{e}^{−{n}} }+\frac{\mathrm{1}}{\mathrm{1}+{e}^{{n}} }\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\left(\frac{{e}^{{n}} +\mathrm{1}}{{e}^{{n}} +\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{99}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathlove last updated on 31/Jan/22

$${thanks} \\ $$
