Question Number 165375 by mathlove last updated on 31/Jan/22
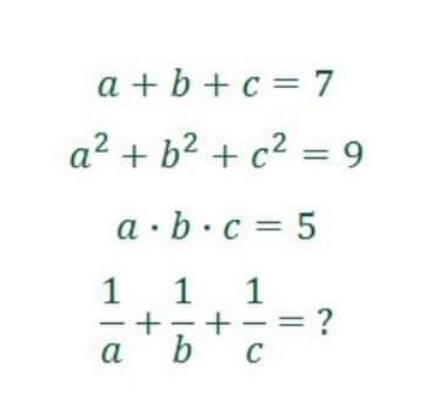
Answered by Rasheed.Sindhi last updated on 31/Jan/22
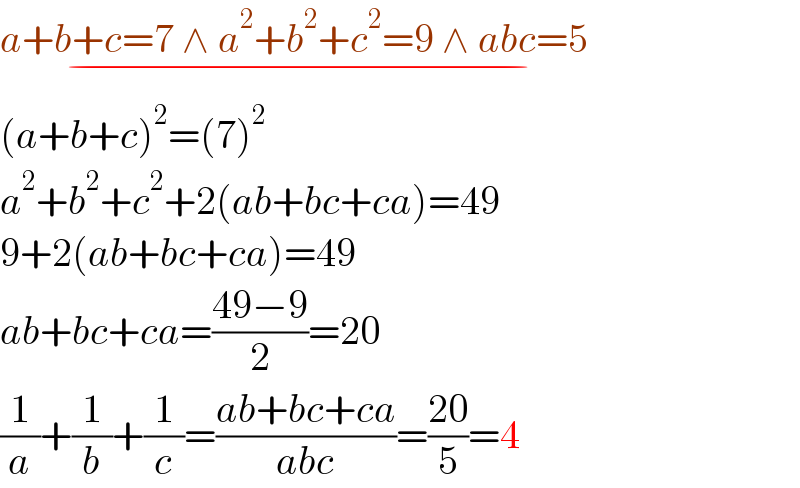
$$\underset{−} {{a}+{b}+{c}=\mathrm{7}\:\wedge\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{9}\:\wedge\:{abc}=\mathrm{5}\:\:\:\:} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\left(\mathrm{7}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{49} \\ $$$$\mathrm{9}+\mathrm{2}\left({ab}+{bc}+{ca}\right)=\mathrm{49} \\ $$$${ab}+{bc}+{ca}=\frac{\mathrm{49}−\mathrm{9}}{\mathrm{2}}=\mathrm{20} \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{{ab}+{bc}+{ca}}{{abc}}=\frac{\mathrm{20}}{\mathrm{5}}=\mathrm{4} \\ $$
Commented by mathlove last updated on 31/Jan/22

$${thanks} \\ $$
