Question Number 165389 by ajfour last updated on 31/Jan/22

Commented by ajfour last updated on 31/Jan/22
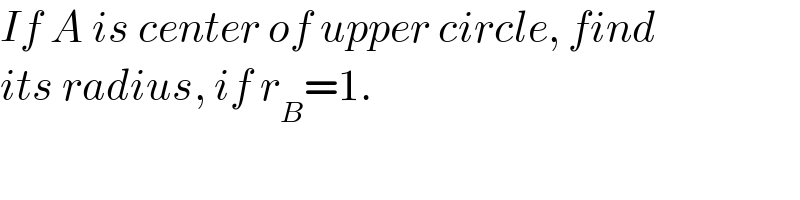
$${If}\:{A}\:{is}\:{center}\:{of}\:{upper}\:{circle},\:{find} \\ $$$${its}\:{radius},\:{if}\:{r}_{{B}} =\mathrm{1}. \\ $$
Answered by mahdipoor last updated on 31/Jan/22
![r_a =a r_b =b d: 0=a+x−y B=(−b,−(√(2ab+a^2 ))) BH=b=((∣a−b+(√(2ab+a^2 ))∣)/( (√2))) ⇒ ±(√2)b=a−b+(√(2ab+a^2 ))⇒(1±(√2))b−a=(√(2ab+a^2 )) (5±2(√2))b^2 +a^2 −(2±2(√2))ab=2ab+a^2 ⇒ b[(5±2(√2))b−(4±2(√2))a]=0⇒ a=((5±2(√2))/(4±2(√2)))b](https://www.tinkutara.com/question/Q165397.png)
$${r}_{{a}} ={a}\:\:\:\:\:{r}_{{b}} ={b} \\ $$$${d}:\:\mathrm{0}={a}+{x}−{y} \\ $$$$\mathrm{B}=\left(−{b},−\sqrt{\mathrm{2}{ab}+{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{BH}={b}=\frac{\mid{a}−{b}+\sqrt{\mathrm{2}{ab}+{a}^{\mathrm{2}} }\mid}{\:\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\pm\sqrt{\mathrm{2}}{b}={a}−{b}+\sqrt{\mathrm{2}{ab}+{a}^{\mathrm{2}} }\Rightarrow\left(\mathrm{1}\pm\sqrt{\mathrm{2}}\right){b}−{a}=\sqrt{\mathrm{2}{ab}+{a}^{\mathrm{2}} } \\ $$$$\left(\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}}\right){b}^{\mathrm{2}} +{a}^{\mathrm{2}} −\left(\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{2}}\right){ab}=\mathrm{2}{ab}+{a}^{\mathrm{2}} \Rightarrow \\ $$$${b}\left[\left(\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}}\right){b}−\left(\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{2}}\right){a}\right]=\mathrm{0}\Rightarrow \\ $$$${a}=\frac{\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{2}}}{b} \\ $$$$ \\ $$
Answered by mr W last updated on 01/Feb/22
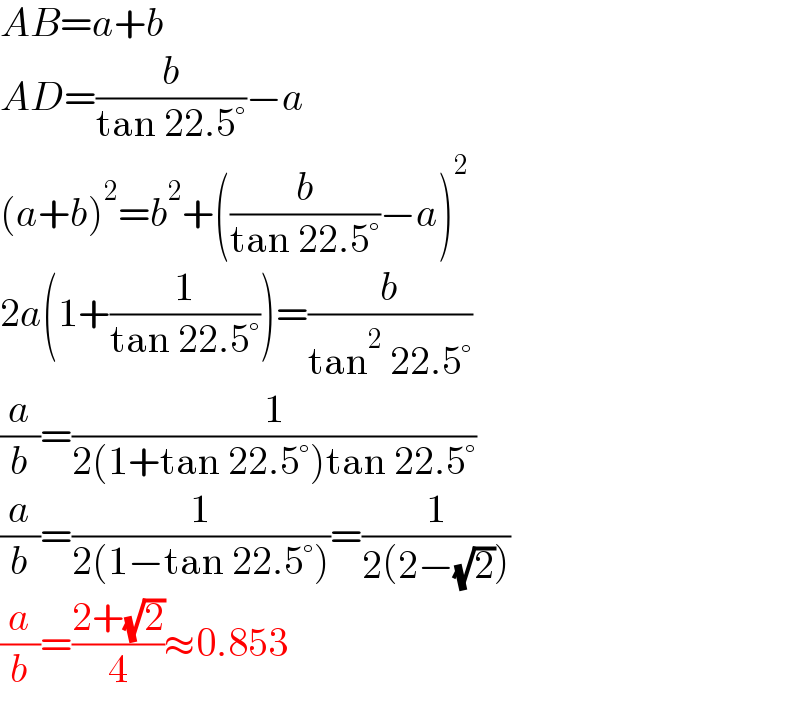
$${AB}={a}+{b} \\ $$$${AD}=\frac{{b}}{\mathrm{tan}\:\mathrm{22}.\mathrm{5}°}−{a} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} +\left(\frac{{b}}{\mathrm{tan}\:\mathrm{22}.\mathrm{5}°}−{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{a}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{22}.\mathrm{5}°}\right)=\frac{{b}}{\mathrm{tan}^{\mathrm{2}} \:\mathrm{22}.\mathrm{5}°} \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{tan}\:\mathrm{22}.\mathrm{5}°\right)\mathrm{tan}\:\mathrm{22}.\mathrm{5}°} \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{tan}\:\mathrm{22}.\mathrm{5}°\right)}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)} \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{853} \\ $$
Commented by mr W last updated on 01/Feb/22
Commented by ajfour last updated on 01/Feb/22
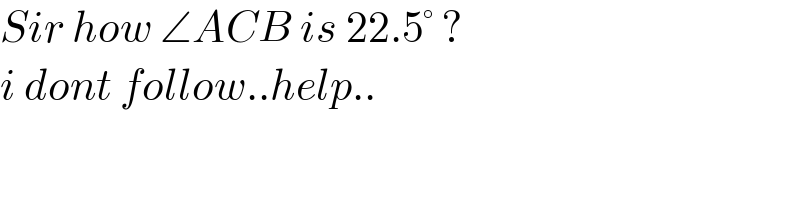
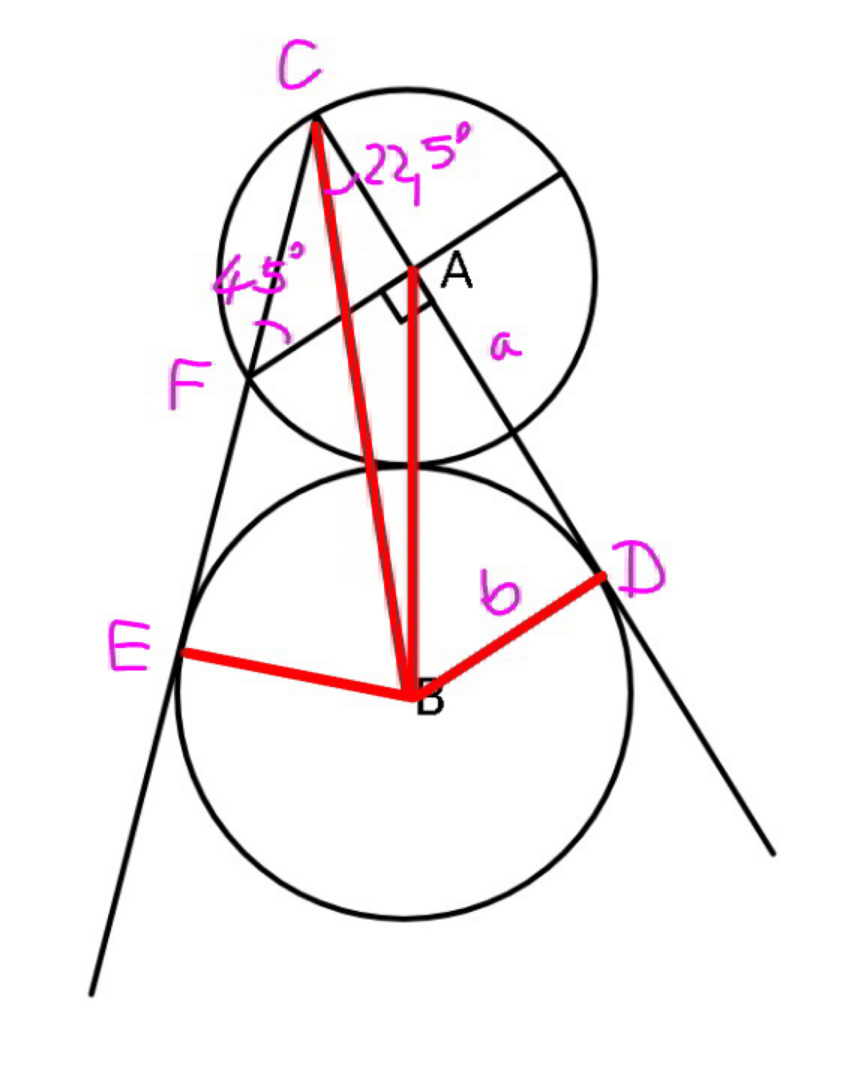
$${Sir}\:{how}\:\angle{ACB}\:{is}\:\mathrm{22}.\mathrm{5}°\:? \\ $$$${i}\:{dont}\:{follow}..{help}.. \\ $$
Commented by mr W last updated on 01/Feb/22
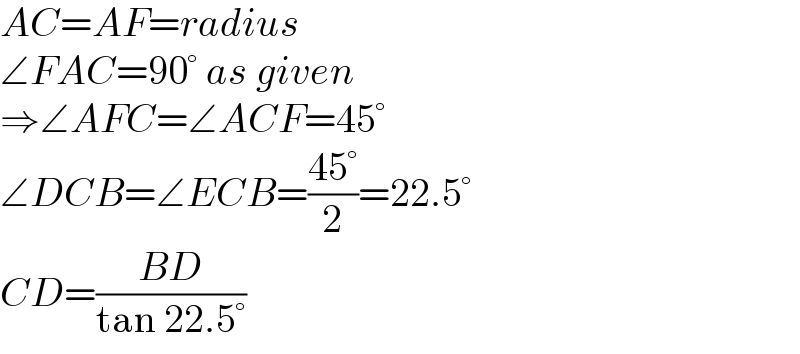
$${AC}={AF}={radius} \\ $$$$\angle{FAC}=\mathrm{90}°\:{as}\:{given} \\ $$$$\Rightarrow\angle{AFC}=\angle{ACF}=\mathrm{45}° \\ $$$$\angle{DCB}=\angle{ECB}=\frac{\mathrm{45}°}{\mathrm{2}}=\mathrm{22}.\mathrm{5}° \\ $$$${CD}=\frac{{BD}}{\mathrm{tan}\:\mathrm{22}.\mathrm{5}°} \\ $$
Commented by ajfour last updated on 01/Feb/22
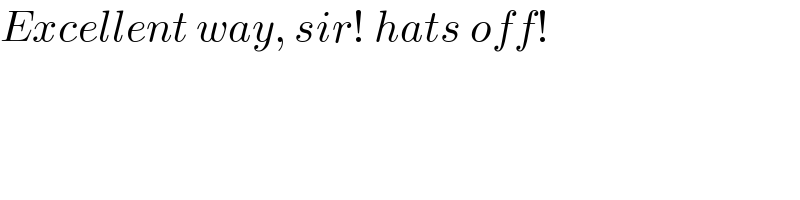
$${Excellent}\:{way},\:{sir}!\:{hats}\:{off}! \\ $$
Commented by Tawa11 last updated on 01/Feb/22

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
