Question Number 165442 by HongKing last updated on 01/Feb/22
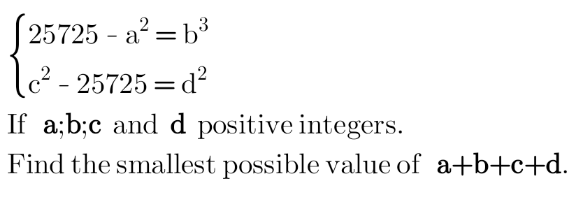
Answered by Rasheed.Sindhi last updated on 02/Feb/22

$$\begin{cases}{\mathrm{25725}−{a}^{\mathrm{2}} ={b}^{\mathrm{3}} }\\{{c}^{\mathrm{2}} −\mathrm{25725}={d}^{\mathrm{2}} }\end{cases}\:\:;\:\:{a},{b},{c},{d}\in\mathbb{Z}^{+} \\ $$$$\underset{−} {\mathcal{T}{he}\:{smallest}\:{a}+{b}+{c}+{d}\:=?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$$\mathcal{T}{he}\:{smallest}\:{a}+{b}+{c}+{d} \\ $$$$\:\:\:\:\:\:\:=\left(\mathcal{T}{he}\:{smallest}\:{a}+{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathcal{T}{he}\:{smallest}\:{c}+{d}\right) \\ $$$$\bullet\:\mathrm{25725}−{a}^{\mathrm{2}} ={b}^{\mathrm{3}} \Rightarrow{a}=\sqrt{\mathrm{25725}−{b}^{\mathrm{3}} }>\mathrm{0} \\ $$$$\Rightarrow\mathrm{25725}−{b}^{\mathrm{3}} >\mathrm{0}\Rightarrow{b}^{\mathrm{3}} <\mathrm{25725} \\ $$$$\Rightarrow{b}<\sqrt[{\mathrm{3}}]{\mathrm{25725}}\:=\mathrm{29}.\mathrm{52}\Rightarrow{b}\leqslant\mathrm{29} \\ $$$${b}=\mathrm{5}\Rightarrow{a}=\mathrm{160}\:\left({the}\:{only}\:{positive}\:{integral}\:{solution}\right) \\ $$$$\underset{−} {\therefore\:\mathcal{T}{he}\:{smallest}\:{a}+{b}=\mathrm{160}+\mathrm{5}=\mathrm{165}\:\:\:\:} \\ $$$$\bullet{c}^{\mathrm{2}} −\mathrm{25725}={d}^{\mathrm{2}} \Rightarrow{c}^{\mathrm{2}} −{d}^{\mathrm{2}} =\mathrm{25725} \\ $$$$\Rightarrow\left({c}−{d}\right)\left({c}+{d}\right)=\mathrm{25725} \\ $$$$\:\Rightarrow{c}+{d}=\frac{\mathrm{25725}}{{c}−{d}} \\ $$$$\mathcal{T}{he}\:{smallest}\:{c}+{d}\Rightarrow\mathcal{T}{he}\:{greatest}\:{c}−{d} \\ $$$$\mathcal{T}{he}\:{greatest}\:{c}−{d}\leqslant\lfloor\sqrt{\mathrm{25725}}\:\rfloor=\mathrm{160} \\ $$$$\mathcal{T}{he}\:{greatest}\:{c}−{d}=\mathrm{147}\:\:\:\: \\ $$$$\underset{−} {\therefore\mathcal{T}{he}\:{smallest}\:{c}+{d}=\mathrm{25765}/\mathrm{147}=\mathrm{175}} \\ $$$$ \\ $$$$\overset{\bullet} {\bullet\:\:\bullet}\:\:\mathcal{T}{he}\:{smallest}\:{a}+{b}+{c}+{d} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{165}\right)+\left(\mathrm{175}\right)=\mathrm{340} \\ $$
Commented by HongKing last updated on 06/Feb/22
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$
