Question-165483

Question Number 165483 by mathlove last updated on 02/Feb/22

Commented by MJS_new last updated on 04/Feb/22

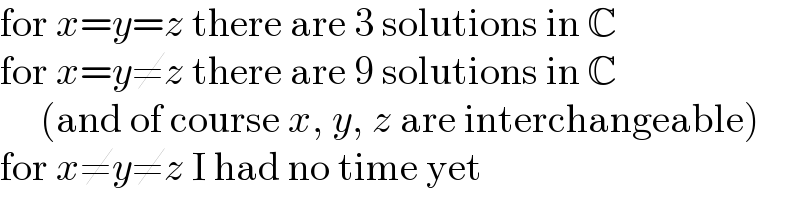
for x=y=z there are 3 solutions in C for x=y≠z there are 9 solutions in C (and of course x, y, z are interchangeable) for x≠y≠z I had no time yet

$$\mathrm{for}\:{x}={y}={z}\:\mathrm{there}\:\mathrm{are}\:\mathrm{3}\:\mathrm{solutions}\:\mathrm{in}\:\mathbb{C} \\ $$$$\mathrm{for}\:{x}={y}\neq{z}\:\mathrm{there}\:\mathrm{are}\:\mathrm{9}\:\mathrm{solutions}\:\mathrm{in}\:\mathbb{C} \\ $$$$\:\:\:\:\:\left(\mathrm{and}\:\mathrm{of}\:\mathrm{course}\:{x},\:{y},\:{z}\:\mathrm{are}\:\mathrm{interchangeable}\right) \\ $$$$\mathrm{for}\:{x}\neq{y}\neq{z}\:\mathrm{I}\:\mathrm{had}\:\mathrm{no}\:\mathrm{time}\:\mathrm{yet} \\ $$

Answered by alephzero last updated on 02/Feb/22

$${x}\:=\:{y}\:=\:{z} \\ $$

Commented by mathlove last updated on 02/Feb/22

$${how}? \\ $$

Commented by alephzero last updated on 02/Feb/22

$$\mathrm{It}'\mathrm{s}\:\mathrm{obvious} \\ $$

Answered by Rasheed.Sindhi last updated on 02/Feb/22

{ ((12x^3 +12y^3 +9z=2......(i))),((12y^3 +12z^3 +9x=2......(ii))),((12z^3 +12x^3 +9y=2... (iii))) :} (i)−(iii):12y^3 −12z^3 +9z−9y=0 12(y−z)(y^2 +yz+z^2 )−9(y−z)=0 (y−z)(12(y^2 +yz+z^2 )−9)=0 y=z ∣ y^2 +yz+z^2 =(3/4) Similarly, (iii)−(ii)⇒z=x ∴ x=y=z

$$\begin{cases}{\mathrm{12}{x}^{\mathrm{3}} +\mathrm{12}{y}^{\mathrm{3}} +\mathrm{9}{z}=\mathrm{2}……\left({i}\right)}\\{\mathrm{12}{y}^{\mathrm{3}} +\mathrm{12}{z}^{\mathrm{3}} +\mathrm{9}{x}=\mathrm{2}……\left({ii}\right)}\\{\mathrm{12}{z}^{\mathrm{3}} +\mathrm{12}{x}^{\mathrm{3}} +\mathrm{9}{y}=\mathrm{2}…\:\:\:\:\left({iii}\right)}\end{cases} \\ $$$$\left({i}\right)−\left({iii}\right):\mathrm{12}{y}^{\mathrm{3}} −\mathrm{12}{z}^{\mathrm{3}} +\mathrm{9}{z}−\mathrm{9}{y}=\mathrm{0} \\ $$$$\mathrm{12}\left({y}−{z}\right)\left({y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} \right)−\mathrm{9}\left({y}−{z}\right)=\mathrm{0} \\ $$$$\left({y}−{z}\right)\left(\mathrm{12}\left({y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} \right)−\mathrm{9}\right)=\mathrm{0} \\ $$$${y}={z}\:\:\mid\:{y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${Similarly}, \\ $$$$\left({iii}\right)−\left({ii}\right)\Rightarrow{z}={x} \\ $$$$\therefore\:{x}={y}={z} \\ $$

Commented by mr W last updated on 03/Feb/22

x=y=z is only one possibitity which gives us 3 solutions. what about other possibilities: x=y≠z x=z≠y y=z≠x x≠y≠z i think we could get more solutions from these possibilities.

$${x}={y}={z}\:{is}\:{only}\:{one}\:{possibitity}\:{which} \\ $$$${gives}\:{us}\:\mathrm{3}\:{solutions}. \\ $$$${what}\:{about}\:{other}\:{possibilities}: \\ $$$${x}={y}\neq{z} \\ $$$${x}={z}\neq{y} \\ $$$${y}={z}\neq{x} \\ $$$${x}\neq{y}\neq{z} \\ $$$${i}\:{think}\:{we}\:{could}\:{get}\:{more}\:{solutions}\: \\ $$$${from}\:{these}\:{possibilities}. \\ $$

Commented by Rasheed.Sindhi last updated on 03/Feb/22

{ ((y−z=0 ∣ y^2 +yz+z^2 =(3/4)....(i))),((x−y=0 ∣ x^2 +xy+y^2 =(3/4)...(ii))),((z−x=0 ∣ z^2 +zx+x^2 =(3/4)...(iii))) :} (ii)−(i): x^2 +xy−yz−z^2 =0 (x−z)(x+z)+y(x−z)=0 (x−z)(x+y+z)=0 x=z ∣ x+y+z=0

$$\begin{cases}{{y}−{z}=\mathrm{0}\:\mid\:{y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}….\left({i}\right)}\\{{x}−{y}=\mathrm{0}\:\mid\:{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}…\left({ii}\right)}\\{{z}−{x}=\mathrm{0}\:\mid\:{z}^{\mathrm{2}} +{zx}+{x}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}…\left({iii}\right)}\end{cases} \\ $$$$\left({ii}\right)−\left({i}\right):\:{x}^{\mathrm{2}} +{xy}−{yz}−{z}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}−{z}\right)\left({x}+{z}\right)+{y}\left({x}−{z}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}−{z}\right)\left({x}+{y}+{z}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}={z}\:\mid\:{x}+{y}+{z}=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply