Question Number 165532 by mathlove last updated on 03/Feb/22
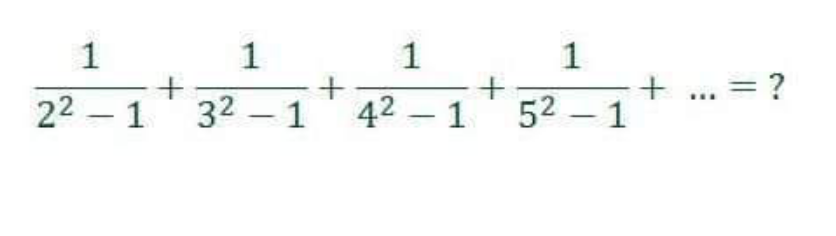
Answered by amin96 last updated on 03/Feb/22
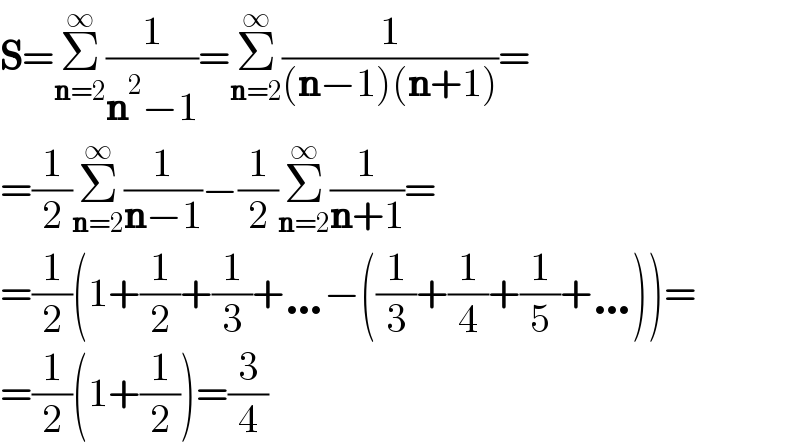
$$\boldsymbol{\mathrm{S}}=\underset{\boldsymbol{\mathrm{n}}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} −\mathrm{1}}=\underset{\boldsymbol{\mathrm{n}}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\ldots−\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+\ldots\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$
