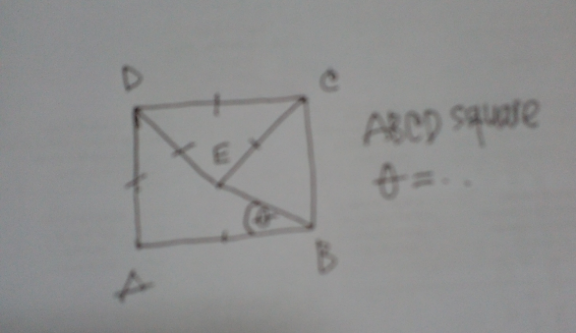
Question Number 165570 by cortano1 last updated on 04/Feb/22
Answered by Rohit143Jo last updated on 04/Feb/22

$$\theta=\mathrm{15}° \\ $$
Answered by Rohit143Jo last updated on 04/Feb/22
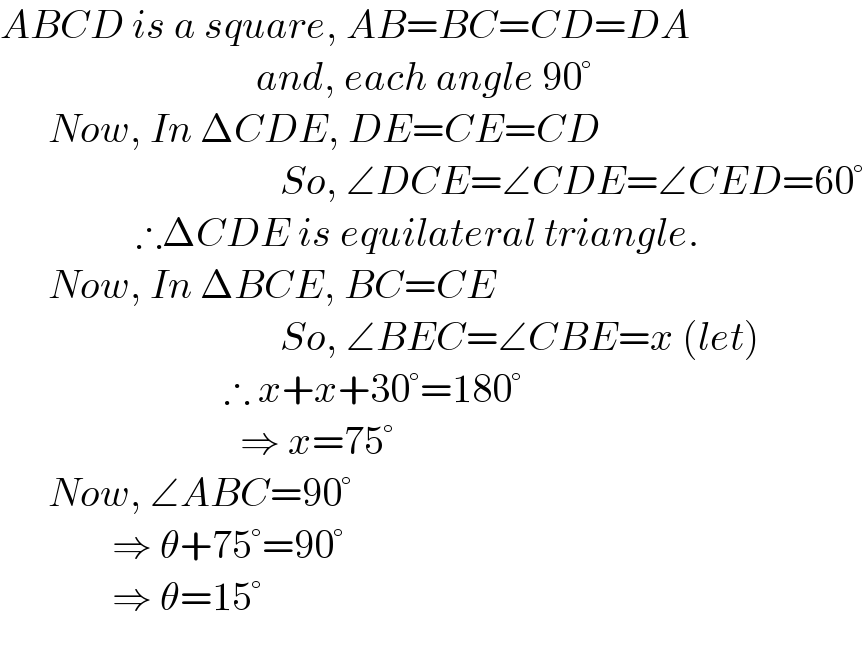
$${ABCD}\:{is}\:{a}\:{square},\:{AB}={BC}={CD}={DA}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{and},\:{each}\:{angle}\:\mathrm{90}° \\ $$$$\:\:\:\:\:\:{Now},\:{In}\:\Delta{CDE},\:{DE}={CE}={CD} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{So},\:\angle{DCE}=\angle{CDE}=\angle{CED}=\mathrm{60}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\Delta{CDE}\:{is}\:{equilateral}\:{triangle}. \\ $$$$\:\:\:\:\:\:{Now},\:{In}\:\Delta{BCE},\:{BC}={CE} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{So},\:\angle{BEC}=\angle{CBE}={x}\:\left({let}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:{x}+{x}+\mathrm{30}°=\mathrm{180}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{x}=\mathrm{75}° \\ $$$$\:\:\:\:\:\:{Now},\:\angle{ABC}=\mathrm{90}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\theta+\mathrm{75}°=\mathrm{90}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\theta=\mathrm{15}° \\ $$
Commented by Tawa11 last updated on 05/Feb/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
