Question Number 165616 by amin96 last updated on 05/Feb/22

Commented by mkam last updated on 06/Feb/22
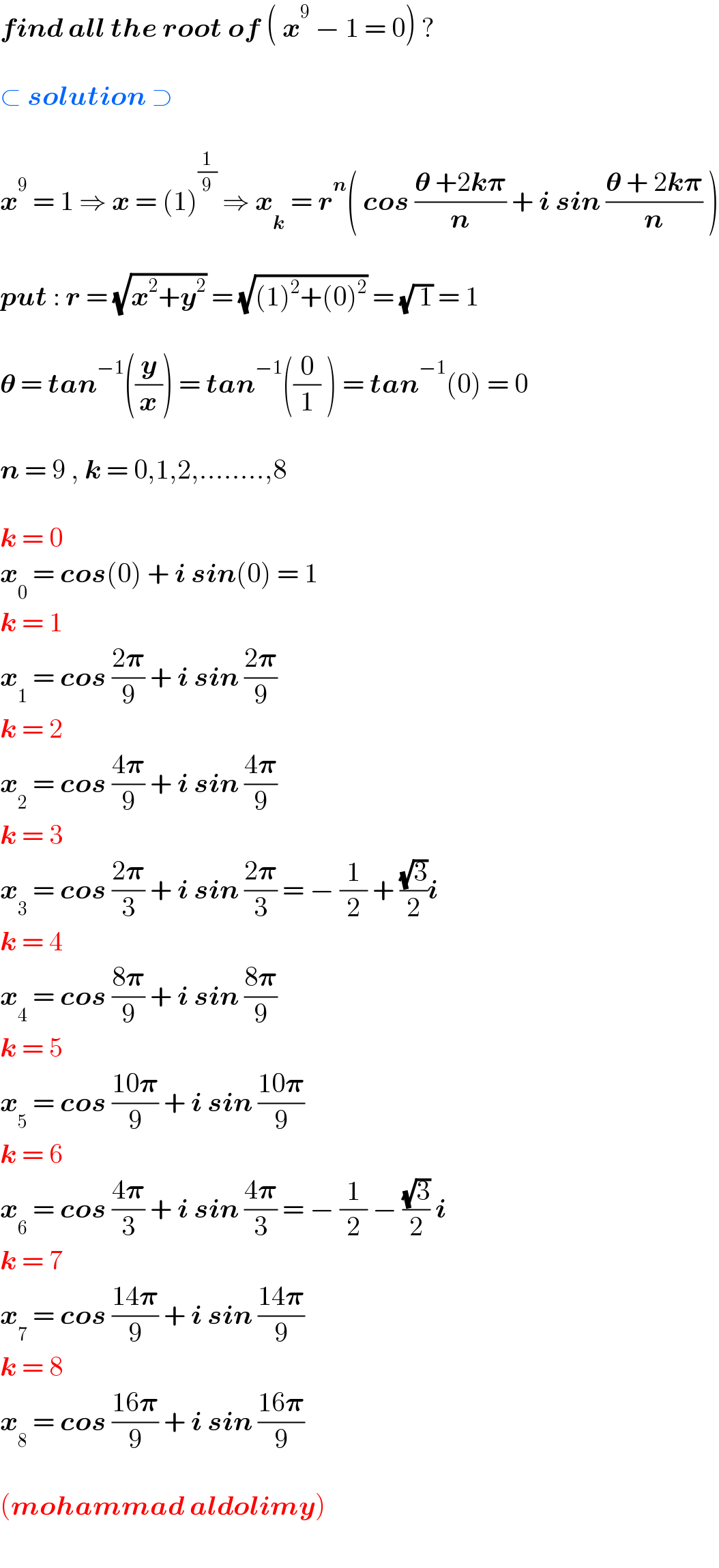
$$\boldsymbol{{find}}\:\boldsymbol{{all}}\:\boldsymbol{{the}}\:\boldsymbol{{root}}\:\boldsymbol{{of}}\:\left(\:\boldsymbol{{x}}^{\mathrm{9}} \:−\:\mathrm{1}\:=\:\mathrm{0}\right)\:? \\ $$$$ \\ $$$$\subset\:\boldsymbol{{solution}}\:\supset \\ $$$$ \\ $$$$\boldsymbol{{x}}^{\mathrm{9}} \:=\:\mathrm{1}\:\Rightarrow\:\boldsymbol{{x}}\:=\:\left(\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{9}}} \:\Rightarrow\:\boldsymbol{{x}}_{\boldsymbol{{k}}} \:=\:\boldsymbol{{r}}^{\boldsymbol{{n}}} \left(\:\boldsymbol{{cos}}\:\frac{\boldsymbol{\theta}\:+\mathrm{2}\boldsymbol{{k}\pi}}{\boldsymbol{{n}}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\boldsymbol{\theta}\:+\:\mathrm{2}\boldsymbol{{k}\pi}}{\boldsymbol{{n}}}\:\right) \\ $$$$ \\ $$$$\boldsymbol{{put}}\::\:\boldsymbol{{r}}\:=\:\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} }\:=\:\sqrt{\left(\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{0}\right)^{\mathrm{2}} }\:=\:\sqrt{\:\mathrm{1}}\:=\:\mathrm{1} \\ $$$$ \\ $$$$\boldsymbol{\theta}\:=\:\boldsymbol{{tan}}^{−\mathrm{1}} \left(\frac{\boldsymbol{{y}}}{\boldsymbol{{x}}}\right)\:=\:\boldsymbol{{tan}}^{−\mathrm{1}} \left(\frac{\mathrm{0}}{\mathrm{1}}\:\right)\:=\:\boldsymbol{{tan}}^{−\mathrm{1}} \left(\mathrm{0}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$$\boldsymbol{{n}}\:=\:\mathrm{9}\:,\:\boldsymbol{{k}}\:=\:\mathrm{0},\mathrm{1},\mathrm{2},……..,\mathrm{8} \\ $$$$ \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{0} \\ $$$$\boldsymbol{{x}}_{\mathrm{0}} \:=\:\boldsymbol{{cos}}\left(\mathrm{0}\right)\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\left(\mathrm{0}\right)\:=\:\mathrm{1} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{1} \\ $$$$\boldsymbol{{x}}_{\mathrm{1}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{9}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{9}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{2} \\ $$$$\boldsymbol{{x}}_{\mathrm{2}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{4}\boldsymbol{\pi}}{\mathrm{9}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{4}\boldsymbol{\pi}}{\mathrm{9}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{3} \\ $$$$\boldsymbol{{x}}_{\mathrm{3}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}}\:=\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\boldsymbol{{i}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{4} \\ $$$$\boldsymbol{{x}}_{\mathrm{4}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{8}\boldsymbol{\pi}}{\mathrm{9}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{8}\boldsymbol{\pi}}{\mathrm{9}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{5} \\ $$$$\boldsymbol{{x}}_{\mathrm{5}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{10}\boldsymbol{\pi}}{\mathrm{9}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{10}\boldsymbol{\pi}}{\mathrm{9}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{6} \\ $$$$\boldsymbol{{x}}_{\mathrm{6}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{4}\boldsymbol{\pi}}{\mathrm{3}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{4}\boldsymbol{\pi}}{\mathrm{3}}\:=\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\boldsymbol{{i}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{7} \\ $$$$\boldsymbol{{x}}_{\mathrm{7}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{14}\boldsymbol{\pi}}{\mathrm{9}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{14}\boldsymbol{\pi}}{\mathrm{9}} \\ $$$$\boldsymbol{{k}}\:=\:\mathrm{8} \\ $$$$\boldsymbol{{x}}_{\mathrm{8}} \:=\:\boldsymbol{{cos}}\:\frac{\mathrm{16}\boldsymbol{\pi}}{\mathrm{9}}\:+\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\:\frac{\mathrm{16}\boldsymbol{\pi}}{\mathrm{9}} \\ $$$$ \\ $$$$\left(\boldsymbol{{mohammad}}\:\boldsymbol{{aldolimy}}\right) \\ $$
Answered by Ar Brandon last updated on 05/Feb/22
![x^9 −1=0 ⇒x^9 =e^(2πik) ⇒x=e^(((2k)/9)iπ) , k∈[0, 8]](https://www.tinkutara.com/question/Q165621.png)
$${x}^{\mathrm{9}} −\mathrm{1}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{9}} ={e}^{\mathrm{2}\pi{ik}} \:\Rightarrow{x}={e}^{\frac{\mathrm{2}{k}}{\mathrm{9}}{i}\pi} \:,\:{k}\in\left[\mathrm{0},\:\mathrm{8}\right] \\ $$
Answered by alephzero last updated on 05/Feb/22

$${x}^{\mathrm{9}} −\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{9}} \:=\:\mathrm{1} \\ $$$${x}\:=\:\mathrm{1} \\ $$
Commented by mkam last updated on 06/Feb/22

$${false} \\ $$
Commented by alephzero last updated on 11/Feb/22
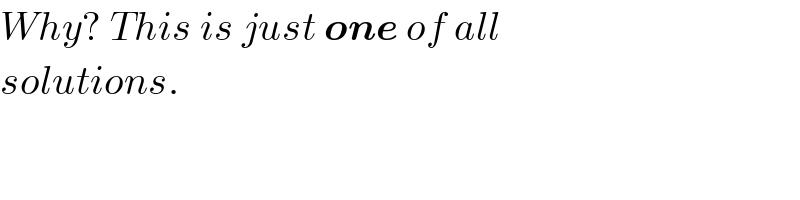
$${Why}?\:{This}\:{is}\:{just}\:\boldsymbol{{one}}\:{of}\:{all} \\ $$$${solutions}. \\ $$
