Question Number 16572 by myintkhaing last updated on 24/Jun/17

Answered by Tinkutara last updated on 24/Jun/17

$$\left(\mathrm{i}\right)\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{series}\:\mathrm{is}\:\mathrm{sin}^{\mathrm{2}} \:{x},\:\mathrm{sin}\:{x},\:\mathrm{1},\:… \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{G}.\mathrm{P}.\:\mathrm{with}\:\mathrm{common}\:\mathrm{ratio} \\ $$$$\mathrm{cosec}\:{x}. \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{7}^{\mathrm{th}} \:\mathrm{term}\:=\:{ar}^{\mathrm{6}} \:=\:\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{sin}^{\mathrm{6}} \:{x}}\:=\:\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{4}} \:{x}}\:=\:\mathrm{16} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}\:=\:\frac{\mathrm{1}}{\mathrm{16}}\:\Rightarrow\:\mathrm{sin}\:{x}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}\:=\:\frac{\pi}{\mathrm{6}}\:,\:\frac{\mathrm{5}\pi}{\mathrm{6}}\:,\:\frac{\mathrm{7}\pi}{\mathrm{6}}\:,\:\frac{\mathrm{11}\pi}{\mathrm{6}} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{part}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear}\:\mathrm{to}\:\mathrm{me}. \\ $$$$\left(\mathrm{iv}\right)\:\mathrm{Since}\:{r}\:=\:\mathrm{cosec}\:{x}\:\mathrm{and}\:\mid\mathrm{cosec}\:{x}\mid\:\geqslant\:\mathrm{1}, \\ $$$$\mathrm{so}\:\mathrm{for}\:\mathrm{sum}\:\mathrm{to}\:\mathrm{infinity}\:\mathrm{to}\:\mathrm{exist}, \\ $$$$\mathrm{cosec}\:{x}\:=\:\mathrm{1}\:\mathrm{for}\:{x}\:=\:\frac{\pi}{\mathrm{2}}\:.\:\mathrm{Now}\:\mathrm{sum}\:\mathrm{to}\:{n} \\ $$$$\mathrm{terms}\:\mathrm{becomes}\:{n}. \\ $$
Commented by myintkhaing last updated on 24/Jun/17

$${Thanks}\:{Sir} \\ $$
Commented by myintkhaing last updated on 24/Jun/17
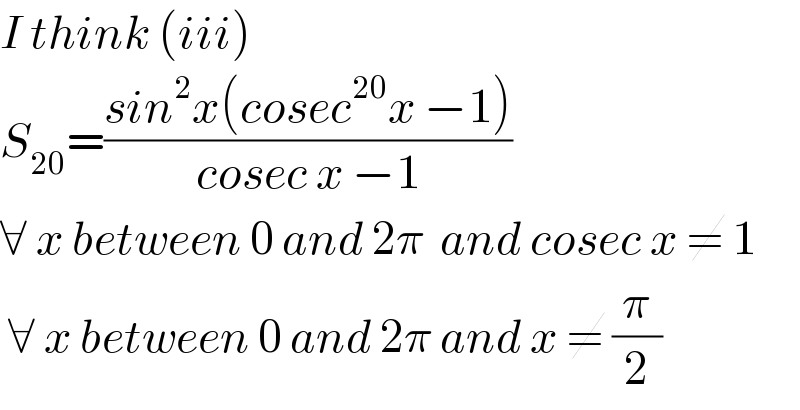
$${I}\:{think}\:\left({iii}\right) \\ $$$${S}_{\mathrm{20}} =\frac{{sin}^{\mathrm{2}} {x}\left({cosec}^{\mathrm{20}} {x}\:−\mathrm{1}\right)}{{cosec}\:{x}\:−\mathrm{1}} \\ $$$$\forall\:{x}\:{between}\:\mathrm{0}\:{and}\:\mathrm{2}\pi\:\:{and}\:{cosec}\:{x}\:\neq\:\mathrm{1} \\ $$$$\:\forall\:{x}\:{between}\:\mathrm{0}\:{and}\:\mathrm{2}\pi\:{and}\:{x}\:\neq\:\frac{\pi}{\mathrm{2}} \\ $$
Commented by Tinkutara last updated on 24/Jun/17
$$\mathrm{Yes}.\:\mathrm{This}\:\mathrm{should}\:\mathrm{be}\:\mathrm{the}\:\mathrm{answer}. \\ $$
