Question Number 165744 by mnjuly1970 last updated on 07/Feb/22

Answered by TheSupreme last updated on 07/Feb/22
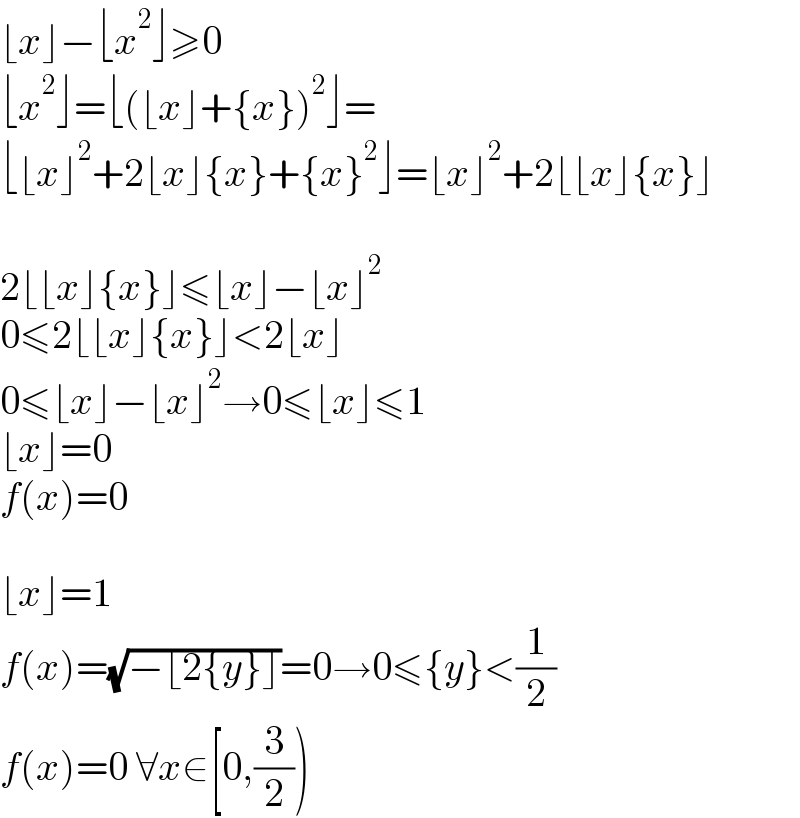
$$\lfloor{x}\rfloor−\lfloor{x}^{\mathrm{2}} \rfloor\geqslant\mathrm{0} \\ $$$$\lfloor{x}^{\mathrm{2}} \rfloor=\lfloor\left(\lfloor{x}\rfloor+\left\{{x}\right\}\right)^{\mathrm{2}} \rfloor= \\ $$$$\lfloor\lfloor{x}\rfloor^{\mathrm{2}} +\mathrm{2}\lfloor{x}\rfloor\left\{{x}\right\}+\left\{{x}\right\}^{\mathrm{2}} \rfloor=\lfloor{x}\rfloor^{\mathrm{2}} +\mathrm{2}\lfloor\lfloor{x}\rfloor\left\{{x}\right\}\rfloor \\ $$$$ \\ $$$$\mathrm{2}\lfloor\lfloor{x}\rfloor\left\{{x}\right\}\rfloor\leqslant\lfloor{x}\rfloor−\lfloor{x}\rfloor^{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant\mathrm{2}\lfloor\lfloor{x}\rfloor\left\{{x}\right\}\rfloor<\mathrm{2}\lfloor{x}\rfloor \\ $$$$\mathrm{0}\leqslant\lfloor{x}\rfloor−\lfloor{x}\rfloor^{\mathrm{2}} \rightarrow\mathrm{0}\leqslant\lfloor{x}\rfloor\leqslant\mathrm{1} \\ $$$$\lfloor{x}\rfloor=\mathrm{0} \\ $$$${f}\left({x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\lfloor{x}\rfloor=\mathrm{1} \\ $$$${f}\left({x}\right)=\sqrt{−\lfloor\mathrm{2}\left\{{y}\right\}\rfloor}=\mathrm{0}\rightarrow\mathrm{0}\leqslant\left\{{y}\right\}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\mathrm{0}\:\forall{x}\in\left[\mathrm{0},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Answered by mahdipoor last updated on 07/Feb/22
![get x=k+a k∈Z 0≤a<1 if k≥0,0≤a<1 { ((0≤a^2 <1)),((0≤2ka<2k)) :} ⇒ 0≤a^2 +2ka<2k+1 ⇒0≤[2ka+a^2 ]≤2k⇒ k^2 ≤[k^2 +2ka+a^2 ]≤k^2 +2k⇒k^2 ≤[x^2 ]≤k^2 +2k so ⇒ −k^2 −k≤[x]−[x^2 ]≤k−k^2 bot [x]−[x^2 ]≥0 ⇒ 0≤[x]−[x^2 ]≤k−k^2 ⇒0≤f(x)≤(√(k−k^2 )) ⇒^(0≤k∈Z) f(x)=0 and if k<0 ⇒ k−k^2 ≤[x]−[x^2 ]≤−k^2 −k ⇒ 0≤f(x)≤(√(−k^2 −k))⇒^(0>k∈Z) f(x)=0 R_f =0](https://www.tinkutara.com/question/Q165754.png)
$${get}\:\:\:{x}={k}+{a}\:\:\:\:{k}\in\mathrm{Z}\:\:\:\:\mathrm{0}\leqslant{a}<\mathrm{1} \\ $$$${if}\:{k}\geqslant\mathrm{0},\mathrm{0}\leqslant{a}<\mathrm{1}\:\begin{cases}{\mathrm{0}\leqslant{a}^{\mathrm{2}} <\mathrm{1}}\\{\mathrm{0}\leqslant\mathrm{2}{ka}<\mathrm{2}{k}}\end{cases}\:\Rightarrow \\ $$$$\mathrm{0}\leqslant{a}^{\mathrm{2}} +\mathrm{2}{ka}<\mathrm{2}{k}+\mathrm{1}\:\Rightarrow\mathrm{0}\leqslant\left[\mathrm{2}{ka}+{a}^{\mathrm{2}} \right]\leqslant\mathrm{2}{k}\Rightarrow \\ $$$${k}^{\mathrm{2}} \leqslant\left[{k}^{\mathrm{2}} +\mathrm{2}{ka}+{a}^{\mathrm{2}} \right]\leqslant{k}^{\mathrm{2}} +\mathrm{2}{k}\Rightarrow{k}^{\mathrm{2}} \leqslant\left[{x}^{\mathrm{2}} \right]\leqslant{k}^{\mathrm{2}} +\mathrm{2}{k} \\ $$$${so}\:\Rightarrow\:−{k}^{\mathrm{2}} −{k}\leqslant\left[{x}\right]−\left[{x}^{\mathrm{2}} \right]\leqslant{k}−{k}^{\mathrm{2}} \\ $$$${bot}\:\left[{x}\right]−\left[{x}^{\mathrm{2}} \right]\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{0}\leqslant\left[{x}\right]−\left[{x}^{\mathrm{2}} \right]\leqslant{k}−{k}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{0}\leqslant{f}\left({x}\right)\leqslant\sqrt{{k}−{k}^{\mathrm{2}} }\:\overset{\mathrm{0}\leqslant{k}\in\mathrm{Z}} {\Rightarrow}\:\:{f}\left({x}\right)=\mathrm{0} \\ $$$${and}\:{if}\:{k}<\mathrm{0}\:\Rightarrow\:{k}−{k}^{\mathrm{2}} \leqslant\left[{x}\right]−\left[{x}^{\mathrm{2}} \right]\leqslant−{k}^{\mathrm{2}} −{k} \\ $$$$\Rightarrow\:\mathrm{0}\leqslant{f}\left({x}\right)\leqslant\sqrt{−{k}^{\mathrm{2}} −{k}}\overset{\mathrm{0}>{k}\in\mathrm{Z}} {\Rightarrow}{f}\left({x}\right)=\mathrm{0}\: \\ $$$${R}_{{f}} =\mathrm{0} \\ $$
