Question Number 165757 by Zaynal last updated on 07/Feb/22

Answered by Mathspace last updated on 08/Feb/22
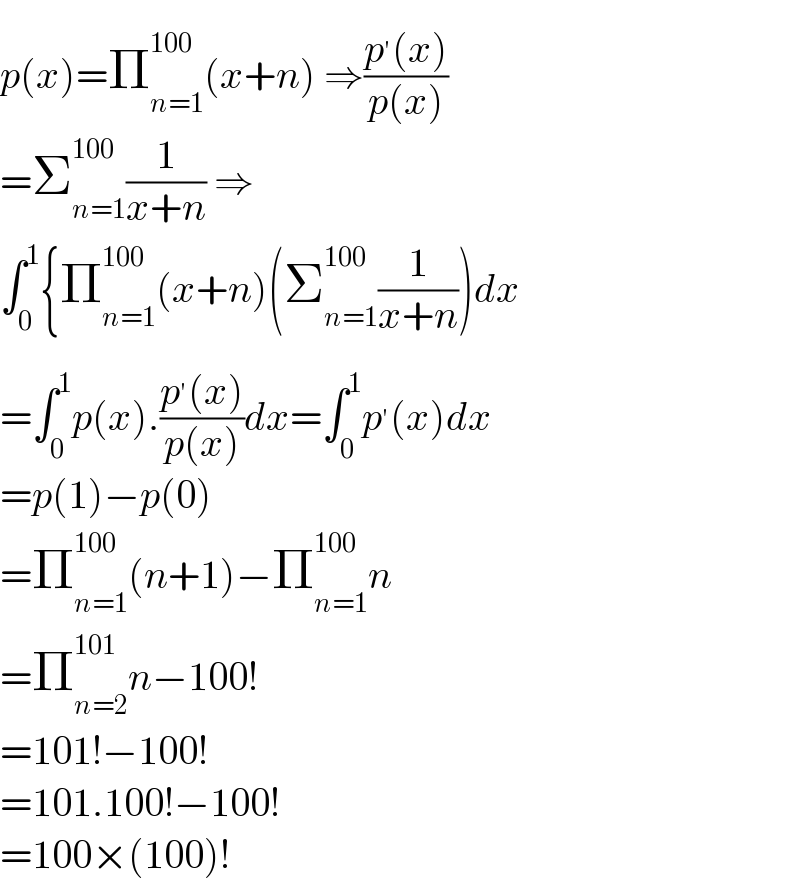
$${p}\left({x}\right)=\prod_{{n}=\mathrm{1}} ^{\mathrm{100}} \left({x}+{n}\right)\:\Rightarrow\frac{{p}^{'} \left({x}\right)}{{p}\left({x}\right)} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\mathrm{100}} \frac{\mathrm{1}}{{x}+{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\prod_{{n}=\mathrm{1}} ^{\mathrm{100}} \left({x}+{n}\right)\left(\sum_{{n}=\mathrm{1}} ^{\mathrm{100}\:} \frac{\mathrm{1}}{{x}+{n}}\right){dx}\right. \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {p}\left({x}\right).\frac{{p}^{'} \left({x}\right)}{{p}\left({x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {p}^{'} \left({x}\right){dx} \\ $$$$={p}\left(\mathrm{1}\right)−{p}\left(\mathrm{0}\right) \\ $$$$=\prod_{{n}=\mathrm{1}} ^{\mathrm{100}} \left({n}+\mathrm{1}\right)−\prod_{{n}=\mathrm{1}} ^{\mathrm{100}} {n} \\ $$$$=\prod_{{n}=\mathrm{2}} ^{\mathrm{101}} {n}−\mathrm{100}! \\ $$$$=\mathrm{101}!−\mathrm{100}! \\ $$$$=\mathrm{101}.\mathrm{100}!−\mathrm{100}! \\ $$$$=\mathrm{100}×\left(\mathrm{100}\right)! \\ $$
