Question Number 16579 by Joel577 last updated on 24/Jun/17

Commented by Joel577 last updated on 24/Jun/17
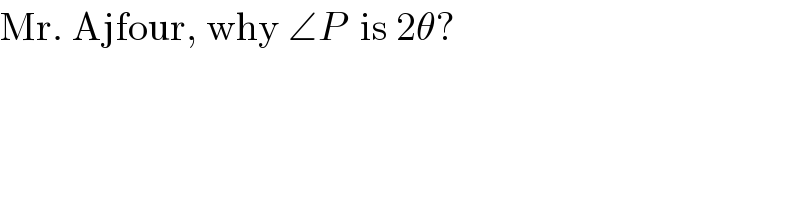
$$\mathrm{Mr}.\:\mathrm{Ajfour},\:\mathrm{why}\:\angle{P}\:\:\mathrm{is}\:\mathrm{2}\theta? \\ $$
Commented by Joel577 last updated on 24/Jun/17

$$\mathrm{pls}\:\mathrm{explain}\:\mathrm{sir} \\ $$
Commented by ajfour last updated on 24/Jun/17
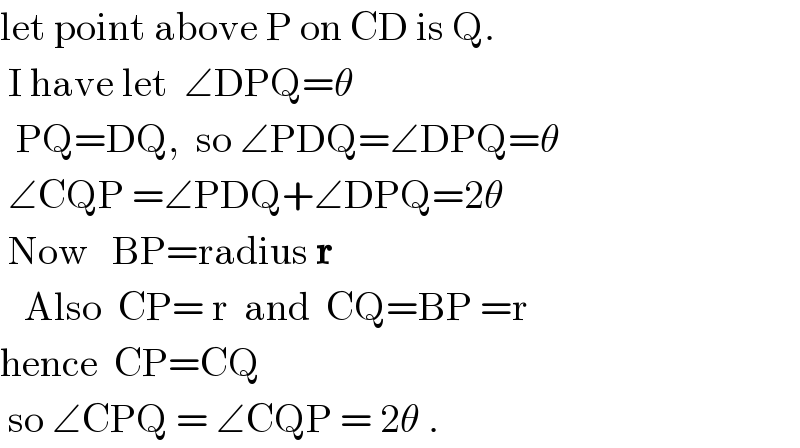
$$\mathrm{let}\:\mathrm{point}\:\mathrm{above}\:\mathrm{P}\:\mathrm{on}\:\mathrm{CD}\:\mathrm{is}\:\mathrm{Q}. \\ $$$$\:\mathrm{I}\:\mathrm{have}\:\mathrm{let}\:\:\angle\mathrm{DPQ}=\theta \\ $$$$\:\:\mathrm{PQ}=\mathrm{DQ},\:\:\mathrm{so}\:\angle\mathrm{PDQ}=\angle\mathrm{DPQ}=\theta \\ $$$$\:\angle\mathrm{CQP}\:=\angle\mathrm{PDQ}+\angle\mathrm{DPQ}=\mathrm{2}\theta \\ $$$$\:\mathrm{Now}\:\:\:\mathrm{BP}=\mathrm{radius}\:\boldsymbol{\mathrm{r}} \\ $$$$\:\:\:\mathrm{Also}\:\:\mathrm{CP}=\:\mathrm{r}\:\:\mathrm{and}\:\:\mathrm{CQ}=\mathrm{BP}\:=\mathrm{r} \\ $$$$\mathrm{hence}\:\:\mathrm{CP}=\mathrm{CQ} \\ $$$$\:\mathrm{so}\:\angle\mathrm{CPQ}\:=\:\angle\mathrm{CQP}\:=\:\mathrm{2}\theta\:. \\ $$
