Menu Close

Question-16595

Tinku Tara 0 Comments
Pin




Question Number 16595 by ajfour last updated on 24/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/Jun/17
you are wellcome dear mr Ajfour.please post your answer.i am waiting for it.
$${you}\:{are}\:{wellcome}\:{dear}\:{mr}\:{Ajfour}.{please}\: \\ $$$${post}\:{your}\:{answer}.{i}\:{am}\:{waiting}\:{for}\:{it}. \\ $$
Commented by ajfour last updated on 24/Jun/17
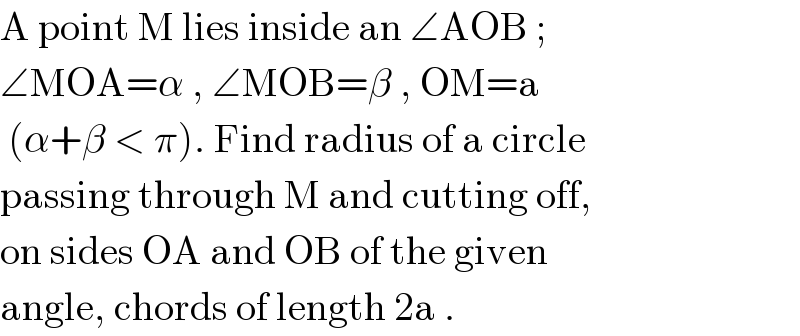
A point M lies inside an ∠AOB ; ∠MOA=α , ∠MOB=β , OM=a (α+β < π). Find radius of a circle passing through M and cutting off, on sides OA and OB of the given angle, chords of length 2a .
$$\mathrm{A}\:\mathrm{point}\:\mathrm{M}\:\mathrm{lies}\:\mathrm{inside}\:\mathrm{an}\:\angle\mathrm{AOB}\:; \\ $$$$\angle\mathrm{MOA}=\alpha\:,\:\angle\mathrm{MOB}=\beta\:,\:\mathrm{OM}=\mathrm{a} \\ $$$$\:\left(\alpha+\beta\:<\:\pi\right).\:\mathrm{Find}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle} \\ $$$$\mathrm{passing}\:\mathrm{through}\:\mathrm{M}\:\mathrm{and}\:\mathrm{cutting}\:\mathrm{off}, \\ $$$$\mathrm{on}\:\mathrm{sides}\:\mathrm{OA}\:\mathrm{and}\:\mathrm{OB}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{angle},\:\mathrm{chords}\:\mathrm{of}\:\mathrm{length}\:\mathrm{2a}\:. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 26/Jun/17
oC=x,oD=y,′P′center of circle.α+β=ϕ C,is the intersect of oB with circle. D,is the intersect of oA with circle. N,is the intersect of oM with circle when continued. op^2 −R^2 =oD.oA=y(2a+y) op^2 −R^2 =oC.o.B=x(2a+x) ⇒y(2a+y)=x(2a+x)⇒x^2 −y^2 +2a(x−y)=0 ⇒(x−y)(x+y+2a)=0⇒x=y=oC=oD. CD^2 =2x^2 −2x^2 cosϕ=4x^2 sin^2 (ϕ/2)⇒ CD=2x.sin(ϕ/2) AB^2 =(x+2a)^2 +(y+2a)^2 −2(x+2a)(y+2a)cosϕu⇒ AB=2(x+2a)sin(ϕ/2) BD^2 =x^2 +(x+2a)^2 −2x(x+2a)cosϕ= =2x^2 +4a^2 +4ax−2x^2 cosϕ−4axcosϕ= =2(x^2 −2ax)(1−cosϕ)+4a^2 = =4(x^2 +2ax)sin^2 (ϕ/2)+4a^2 ⇒BD=2(√(a^2 +(x^2 +2ax)sin^2 (ϕ/2))) CA=2(√(a^2 +(x^2 +2ax)sin^2 (ϕ/2))) DM^2 =a^2 +x^2 −2axcosα CM^2 =a^2 +x^2 −2axcosβ AM^2 =a^2 +(2a+x)^2 −2x(2a+x)cosα (x+2a)(DM^2 +2ax)=2a.a^2 +x.AM^2 (x+2a)(a^2 +x^2 −2axcosα+2ax)=2a^3 +x[a^2 +(2a+x)^2 −2x(2a+x)cosα]⇒ xa^2 +x^3 −2ax^2 cosα+2ax^2 +2a^3 +2ax^2 −4a^2 xcosα+4a^2 x= =2a^3 +xa^2 +x(2a+x)^2 −2x^2 (2a+x)cosα ⇒−2ax^2 cosα−2x^3 cosα+4a^2 xcosα=0 ⇒x^2 +ax−2a^2 =0⇒x=((−a±(√(a^2 +8a^2 )))/2) ⇒x=y=((−a+3a)/2)=a CD=2asin(ϕ/2),AB=6asin(ϕ/2), BD=CA=2a(√(1+3sin^2 (ϕ/2))) DM=2asin(α/2),CM=2asin(β/2) a^2 =a^2 +DM^2 −2a.DM.cos(oDM) ⇒cos(oDM)=((DM)/(2a))=((2asin(α/2))/(2a))=sin(α/2) ⇒oDM=(π/2)−(α/2) MB^2 =MD^2 +BD^2 −2MD.BD.cos(MDB) MB^2 =a^2 +9a^2 −6a^2 cosβ=2a^2 (5−3cosβ) 10a^2 −6a^2 cosβ=4a^2 sin^2 (α/2)+4a^2 (1+3sin^2 (ϕ/2))−8a^2 sin(α/2)(√(1+3sin^2 (ϕ/2))).cos(MDB) 2a^2 −6a^2 cosβ+2a^2 cosα−6a^2 cos(α+β)=−8a^2 sin(α/2)(√(1+3sin^2 ((α+β)/2))).cos(MDB) ⇒^ cos(MDB)=(√2).((3cos(α+β)+3cosβ−cosα−1)/(2sin(α/2).(√(5−3cos(α+β)))))
$${oC}={x},{oD}={y},'{P}'{center}\:{of}\:{circle}.\alpha+\beta=\varphi \\ $$$${C},{is}\:{the}\:{intersect}\:{of}\:{oB}\:{with}\:{circle}. \\ $$$${D},{is}\:{the}\:{intersect}\:{of}\:{oA}\:{with}\:{circle}. \\ $$$${N},{is}\:{the}\:{intersect}\:{of}\:{oM}\:{with}\:{circle}\: \\ $$$${when}\:{continued}. \\ $$$${op}^{\mathrm{2}} −{R}^{\mathrm{2}} ={oD}.{oA}={y}\left(\mathrm{2}{a}+{y}\right) \\ $$$${op}^{\mathrm{2}} −{R}^{\mathrm{2}} ={oC}.{o}.{B}={x}\left(\mathrm{2}{a}+{x}\right) \\ $$$$\Rightarrow{y}\left(\mathrm{2}{a}+{y}\right)={x}\left(\mathrm{2}{a}+{x}\right)\Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{2}{a}\left({x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}−{y}\right)\left({x}+{y}+\mathrm{2}{a}\right)=\mathrm{0}\Rightarrow{x}={y}={oC}={oD}. \\ $$$${CD}^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {cos}\varphi=\mathrm{4}{x}^{\mathrm{2}} {sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}\Rightarrow \\ $$$${CD}=\mathrm{2}{x}.{sin}\frac{\varphi}{\mathrm{2}} \\ $$$${AB}^{\mathrm{2}} =\left({x}+\mathrm{2}{a}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{2}\left({x}+\mathrm{2}{a}\right)\left({y}+\mathrm{2}{a}\right){cos}\varphi{u}\Rightarrow \\ $$$${AB}=\mathrm{2}\left({x}+\mathrm{2}{a}\right){sin}\frac{\varphi}{\mathrm{2}} \\ $$$${BD}^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({x}+\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{2}{x}\left({x}+\mathrm{2}{a}\right){cos}\varphi= \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{ax}−\mathrm{2}{x}^{\mathrm{2}} {cos}\varphi−\mathrm{4}{axcos}\varphi= \\ $$$$=\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{2}{ax}\right)\left(\mathrm{1}−{cos}\varphi\right)+\mathrm{4}{a}^{\mathrm{2}} = \\ $$$$=\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{2}{ax}\right){sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}+\mathrm{4}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{BD}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\mathrm{2}{ax}\right){sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}} \\ $$$${CA}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\mathrm{2}{ax}\right){sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}} \\ $$$${DM}^{\mathrm{2}} ={a}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{axcos}\alpha \\ $$$${CM}^{\mathrm{2}} ={a}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{axcos}\beta \\ $$$${AM}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\mathrm{2}{a}+{x}\right)^{\mathrm{2}} −\mathrm{2}{x}\left(\mathrm{2}{a}+{x}\right){cos}\alpha \\ $$$$\left({x}+\mathrm{2}{a}\right)\left({DM}^{\mathrm{2}} +\mathrm{2}{ax}\right)=\mathrm{2}{a}.{a}^{\mathrm{2}} +{x}.{AM}^{\mathrm{2}} \\ $$$$\left({x}+\mathrm{2}{a}\right)\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{axcos}\alpha+\mathrm{2}{ax}\right)=\mathrm{2}{a}^{\mathrm{3}} +{x}\left[{a}^{\mathrm{2}} +\left(\mathrm{2}{a}+{x}\right)^{\mathrm{2}} −\mathrm{2}{x}\left(\mathrm{2}{a}+{x}\right){cos}\alpha\right]\Rightarrow \\ $$$${xa}^{\mathrm{2}} +{x}^{\mathrm{3}} −\mathrm{2}{ax}^{\mathrm{2}} {cos}\alpha+\mathrm{2}{ax}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{3}} +\mathrm{2}{ax}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {xcos}\alpha+\mathrm{4}{a}^{\mathrm{2}} {x}= \\ $$$$=\mathrm{2}{a}^{\mathrm{3}} +{xa}^{\mathrm{2}} +{x}\left(\mathrm{2}{a}+{x}\right)^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} \left(\mathrm{2}{a}+{x}\right){cos}\alpha \\ $$$$\Rightarrow−\mathrm{2}{ax}^{\mathrm{2}} {cos}\alpha−\mathrm{2}{x}^{\mathrm{3}} {cos}\alpha+\mathrm{4}{a}^{\mathrm{2}} {xcos}\alpha=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{ax}−\mathrm{2}{a}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\frac{−{a}\pm\sqrt{{a}^{\mathrm{2}} +\mathrm{8}{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{x}={y}=\frac{−{a}+\mathrm{3}{a}}{\mathrm{2}}={a} \\ $$$${CD}=\mathrm{2}{asin}\frac{\varphi}{\mathrm{2}},{AB}=\mathrm{6}{asin}\frac{\varphi}{\mathrm{2}}, \\ $$$${BD}={CA}=\mathrm{2}{a}\sqrt{\mathrm{1}+\mathrm{3}{sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}} \\ $$$${DM}=\mathrm{2}{asin}\frac{\alpha}{\mathrm{2}},{CM}=\mathrm{2}{asin}\frac{\beta}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} ={a}^{\mathrm{2}} +{DM}^{\mathrm{2}} −\mathrm{2}{a}.{DM}.{cos}\left({oDM}\right) \\ $$$$\Rightarrow{cos}\left({oDM}\right)=\frac{{DM}}{\mathrm{2}{a}}=\frac{\mathrm{2}{asin}\frac{\alpha}{\mathrm{2}}}{\mathrm{2}{a}}={sin}\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow{oDM}=\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}} \\ $$$${MB}^{\mathrm{2}} ={MD}^{\mathrm{2}} +{BD}^{\mathrm{2}} −\mathrm{2}{MD}.{BD}.{cos}\left({MDB}\right) \\ $$$${MB}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{9}{a}^{\mathrm{2}} −\mathrm{6}{a}^{\mathrm{2}} {cos}\beta=\mathrm{2}{a}^{\mathrm{2}} \left(\mathrm{5}−\mathrm{3}{cos}\beta\right) \\ $$$$\mathrm{10}{a}^{\mathrm{2}} −\mathrm{6}{a}^{\mathrm{2}} {cos}\beta=\mathrm{4}{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}+\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}\right)−\mathrm{8}{a}^{\mathrm{2}} {sin}\frac{\alpha}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{3}{sin}^{\mathrm{2}} \frac{\varphi}{\mathrm{2}}}.{cos}\left({MDB}\right) \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\mathrm{6}{a}^{\mathrm{2}} {cos}\beta+\mathrm{2}{a}^{\mathrm{2}} {cos}\alpha−\mathrm{6}{a}^{\mathrm{2}} {cos}\left(\alpha+\beta\right)=−\mathrm{8}{a}^{\mathrm{2}} {sin}\frac{\alpha}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{3}{sin}^{\mathrm{2}} \frac{\alpha+\beta}{\mathrm{2}}}.{cos}\left({MDB}\right) \\ $$$$\overset{} {\Rightarrow}{cos}\left({MDB}\right)=\sqrt{\mathrm{2}}.\frac{\mathrm{3}{cos}\left(\alpha+\beta\right)+\mathrm{3}{cos}\beta−{cos}\alpha−\mathrm{1}}{\mathrm{2}{sin}\frac{\alpha}{\mathrm{2}}.\sqrt{\mathrm{5}−\mathrm{3}{cos}\left(\alpha+\beta\right)}} \\ $$
Commented by ajfour last updated on 25/Jun/17
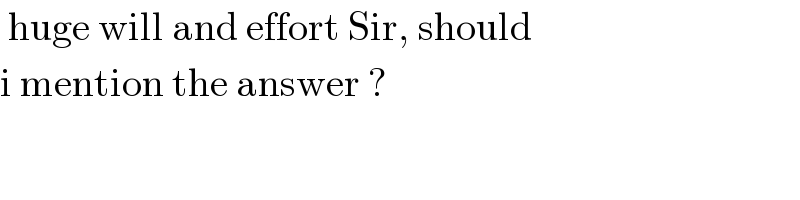
huge will and effort Sir, should i mention the answer ?
$$\:\mathrm{huge}\:\mathrm{will}\:\mathrm{and}\:\mathrm{effort}\:\mathrm{Sir},\:\mathrm{should} \\ $$$$\mathrm{i}\:\mathrm{mention}\:\mathrm{the}\:\mathrm{answer}\:? \\ $$
Answered by ajfour last updated on 25/Jun/17
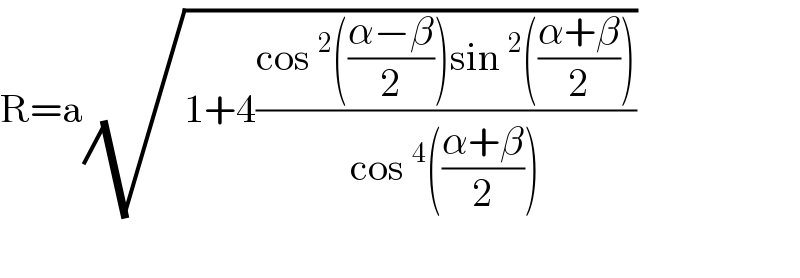
R=a(√(1+4((cos^2 (((α−β)/2))sin^2 (((α+β)/2)))/(cos^4 (((α+β)/2))))))
$$\mathrm{R}=\mathrm{a}\sqrt{\mathrm{1}+\mathrm{4}\frac{\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\alpha−\beta}{\mathrm{2}}\right)\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\alpha+\beta}{\mathrm{2}}\right)}{\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\alpha+\beta}{\mathrm{2}}\right)}}\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *