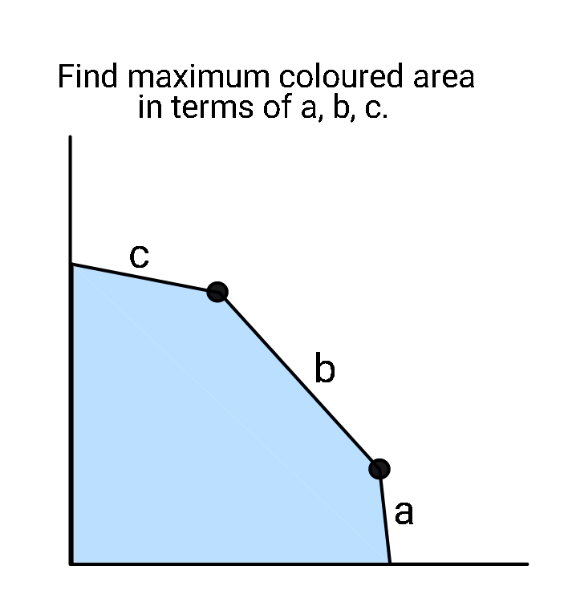
Question Number 165965 by ajfour last updated on 10/Feb/22
Answered by mr W last updated on 10/Feb/22

Commented by mr W last updated on 12/Feb/22

$${A}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} \\ $$$${A}_{\mathrm{1}} \:{is}\:{maximum}\:{when}\:{p}={q}=\frac{{x}}{\:\sqrt{\mathrm{2}}}. \\ $$$${A}_{\mathrm{1},{max}} =\frac{{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${A}_{\mathrm{2}} \:{is}\:{maximum}\:{when}\:{the}\:{quadrilateral} \\ $$$${is}\:{cyclic}. \\ $$$${A}_{\mathrm{2},{max}} =\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{x}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}+{x}}{\mathrm{2}}. \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\frac{\left({ab}+{cd}\right)\left({ac}+{bd}\right)\left({ad}+{bc}\right)}{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right)}} \\ $$$${with}\:{d}={x}. \\ $$$${A}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{x}\right)} \\ $$$${such}\:{that}\:{A}\:{is}\:{maximum}, \\ $$$$\frac{{dA}}{{dx}}=\frac{{x}}{\mathrm{2}}+\frac{\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{x}\right)}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{s}−{a}}+\frac{\mathrm{1}}{{s}−{b}}+\frac{\mathrm{1}}{{s}−{c}}−\frac{\mathrm{1}}{{s}−{x}}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{x}+\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{x}\right)}\left(\frac{\mathrm{1}}{{s}−{a}}+\frac{\mathrm{1}}{{s}−{b}}+\frac{\mathrm{1}}{{s}−{c}}−\frac{\mathrm{1}}{{s}−{x}}\right)=\mathrm{0} \\ $$$$….\:{exact}\:{solution}\:{for}\:{x}\:{seems} \\ $$$${impossible}… \\ $$$$ \\ $$$${example}:\:{a}=\mathrm{1},\:{b}=\mathrm{3},\:{c}=\mathrm{2} \\ $$$$\Rightarrow{x}\approx\mathrm{5}.\mathrm{4969},\:{A}_{{max}} \approx\mathrm{11}.\mathrm{062} \\ $$
Commented by mr W last updated on 11/Feb/22

Commented by mr W last updated on 11/Feb/22

Commented by mr W last updated on 11/Feb/22

Commented by mr W last updated on 11/Feb/22

Commented by Tawa11 last updated on 11/Feb/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by aleks041103 last updated on 12/Feb/22

$${The}\:{approach}\:{you}\:{take}\:{up}\:{is}\:{the}\:{same} \\ $$$${to}\:{what}\:{I}\:{had}\:{in}\:{mind},\:{but}\:{still}\:{I}\:{have} \\ $$$${an}\:{objection}. \\ $$$${You}\:{maximized}\:{A}_{\mathrm{1}} \:{for}\:{a}\:{given}\:{x},\:{and} \\ $$$${then}\:{you}\:{seem}\:{to}\:{imply}\:{that}\:{if}\:{A}_{\mathrm{2}} \:{is}\:{max} \\ $$$${then}\:{A}={A}_{\mathrm{1}} +{A}_{\mathrm{2}} \:{will}\:{be}\:{max},\:{which} \\ $$$${isn}'{t}\:{nessecairly}\:{true}. \\ $$$${Basically},\:{you}\:{say}\:{that}: \\ $$$${A}\left({x}\right)={A}_{\mathrm{1}\:{max}} \left({x}\right)+{A}_{\mathrm{2}\:{max}} \left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{A}_{\mathrm{2}\:{max}} \left({x}\right) \\ $$$${is}\:{max}\:{when}\:{A}_{\mathrm{2}\:{max}\:} \left({x}\right)\:{is}\:{max}. \\ $$$${This}\:{is}\:{obviously}\:{not}\:{true},\:{since}: \\ $$$${A}\:{is}\:{max}\Rightarrow{A}'=\mathrm{0} \\ $$$${but} \\ $$$${A}'=\frac{{x}}{\mathrm{2}}+{A}_{\mathrm{2}{max}} '=\mathrm{0}\nLeftrightarrow{A}_{\mathrm{2}{max}} '=\mathrm{0} \\ $$
Commented by mr W last updated on 12/Feb/22

$${i}\:{didn}'{t}\:{say}\:{that}\:{A}\:{is}\:{maximum}\:{if}\:{A}_{\mathrm{2}} \: \\ $$$${is}\:{maximum}.\:{you}\:{can}\:{see}\:{that}\:{i} \\ $$$${set}\:{A}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{x}\right)} \\ $$$${and}\:{request}\:\frac{{dA}}{{dx}}=\mathrm{0}. \\ $$$${when}\:{we}\:{have}\:{four}\:{sides}\:{a},{b},{c},{x},\:{it}'{s} \\ $$$${clear}\:{that}\:{A}_{\mathrm{1}} \:{should}\:{be}\:{an}\:{isosceles}\: \\ $$$${right}\:{triangle}\:{with}\:{area}\:\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:{and}\:{the} \\ $$$${quatrilateral}\:{should}\:{be}\:{a}\:{cyclic}\:{one} \\ $$$${with}\:{area}\:\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{x}\right)}. \\ $$$${the}\:{sum}\:{of}\:{both}\:{should}\:{be}\:{maximum}. \\ $$
Commented by mr W last updated on 12/Feb/22
$${the}\:{solution}\:{could}\:{be}\:{much}\:{easier}\:{if} \\ $$$${we}\:{just}\:{request}\:{that}\:{A}_{\mathrm{2}} \:{should}\:{be} \\ $$$${maximum},\:{see}\:{Q}\mathrm{166007}. \\ $$
Commented by aleks041103 last updated on 12/Feb/22

$${Yes},\:{you}'{re}\:{right}!\:{I}'{m}\:{sorry},\:{I} \\ $$$${misunderstood}\:{your}\:{solution}! \\ $$$${It}'{s}\:{fine}!\:{Sorry}\:{again}! \\ $$
Commented by mr W last updated on 12/Feb/22
$${it}'{s}\:{alright}\:{sir}.\:{i}\:{appreciate}\:{such} \\ $$$${substantial}\:{feedback}\:{very}\:{much}. \\ $$$${thanks}\:{alot}! \\ $$
Commented by mr W last updated on 12/Feb/22
Commented by mr W last updated on 12/Feb/22
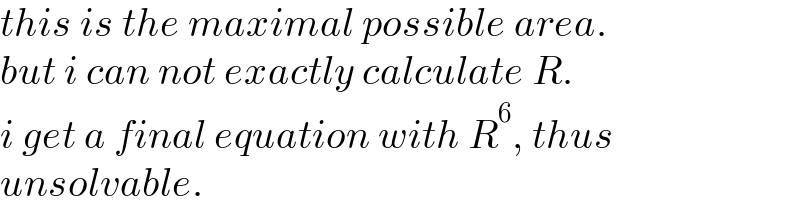
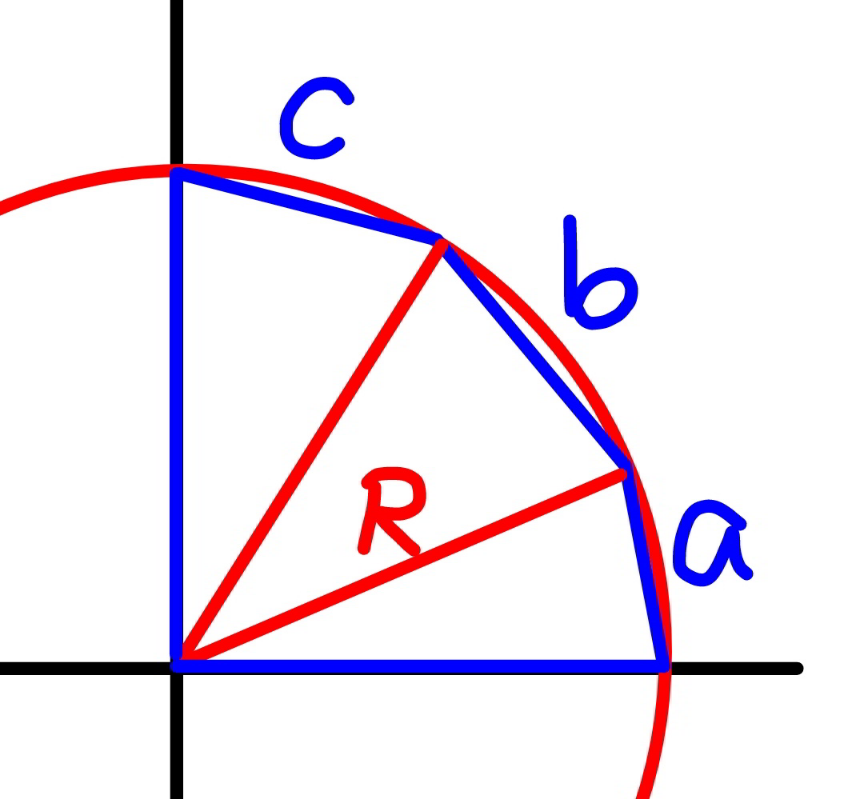
$${this}\:{is}\:{the}\:{maximal}\:{possible}\:{area}. \\ $$$${but}\:{i}\:{can}\:{not}\:{exactly}\:{calculate}\:{R}. \\ $$$${i}\:{get}\:{a}\:{final}\:{equation}\:{with}\:{R}^{\mathrm{6}} ,\:{thus} \\ $$$${unsolvable}. \\ $$
Commented by mr W last updated on 12/Feb/22
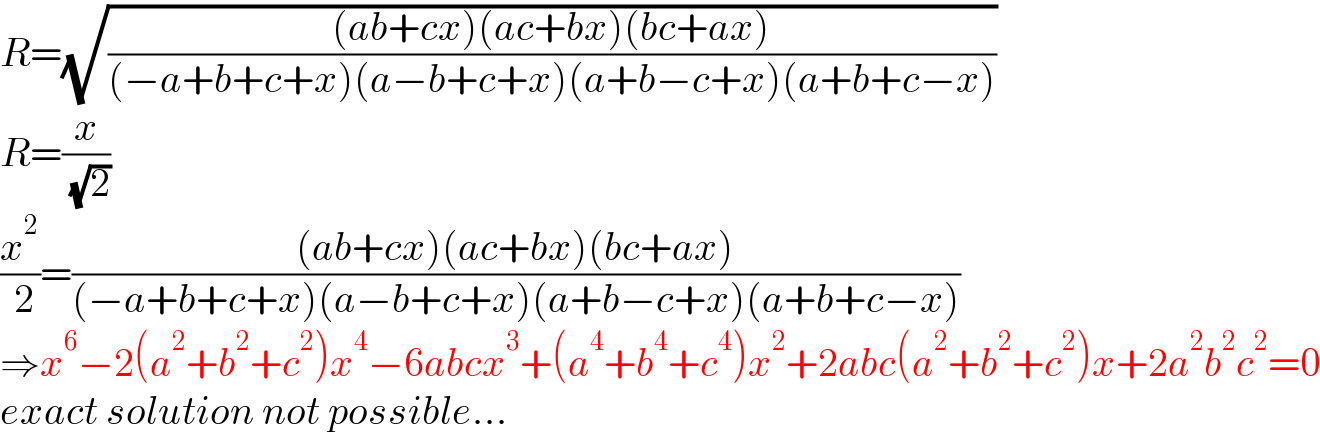
$${R}=\sqrt{\frac{\left({ab}+{cx}\right)\left({ac}+{bx}\right)\left({bc}+{ax}\right)}{\left(−{a}+{b}+{c}+{x}\right)\left({a}−{b}+{c}+{x}\right)\left({a}+{b}−{c}+{x}\right)\left({a}+{b}+{c}−{x}\right)}} \\ $$$${R}=\frac{{x}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{{x}^{\mathrm{2}} }{\:\mathrm{2}}=\frac{\left({ab}+{cx}\right)\left({ac}+{bx}\right)\left({bc}+{ax}\right)}{\left(−{a}+{b}+{c}+{x}\right)\left({a}−{b}+{c}+{x}\right)\left({a}+{b}−{c}+{x}\right)\left({a}+{b}+{c}−{x}\right)} \\ $$$$\Rightarrow{x}^{\mathrm{6}} −\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){x}^{\mathrm{4}} −\mathrm{6}{abcx}^{\mathrm{3}} +\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right){x}^{\mathrm{2}} +\mathrm{2}{abc}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){x}+\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{0} \\ $$$${exact}\:{solution}\:{not}\:{possible}… \\ $$
Answered by ajfour last updated on 11/Feb/22

