Question Number 165984 by nurtani last updated on 10/Feb/22
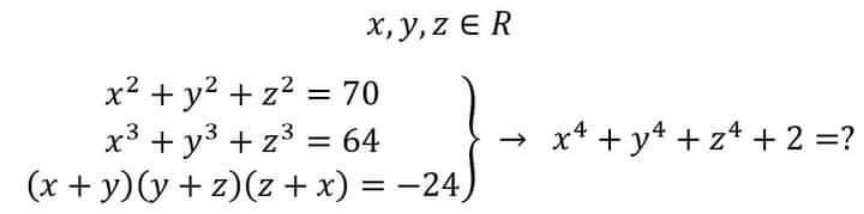
Commented by cortano1 last updated on 10/Feb/22

$$\mathrm{2024} \\ $$
Answered by Rasheed.Sindhi last updated on 11/Feb/22
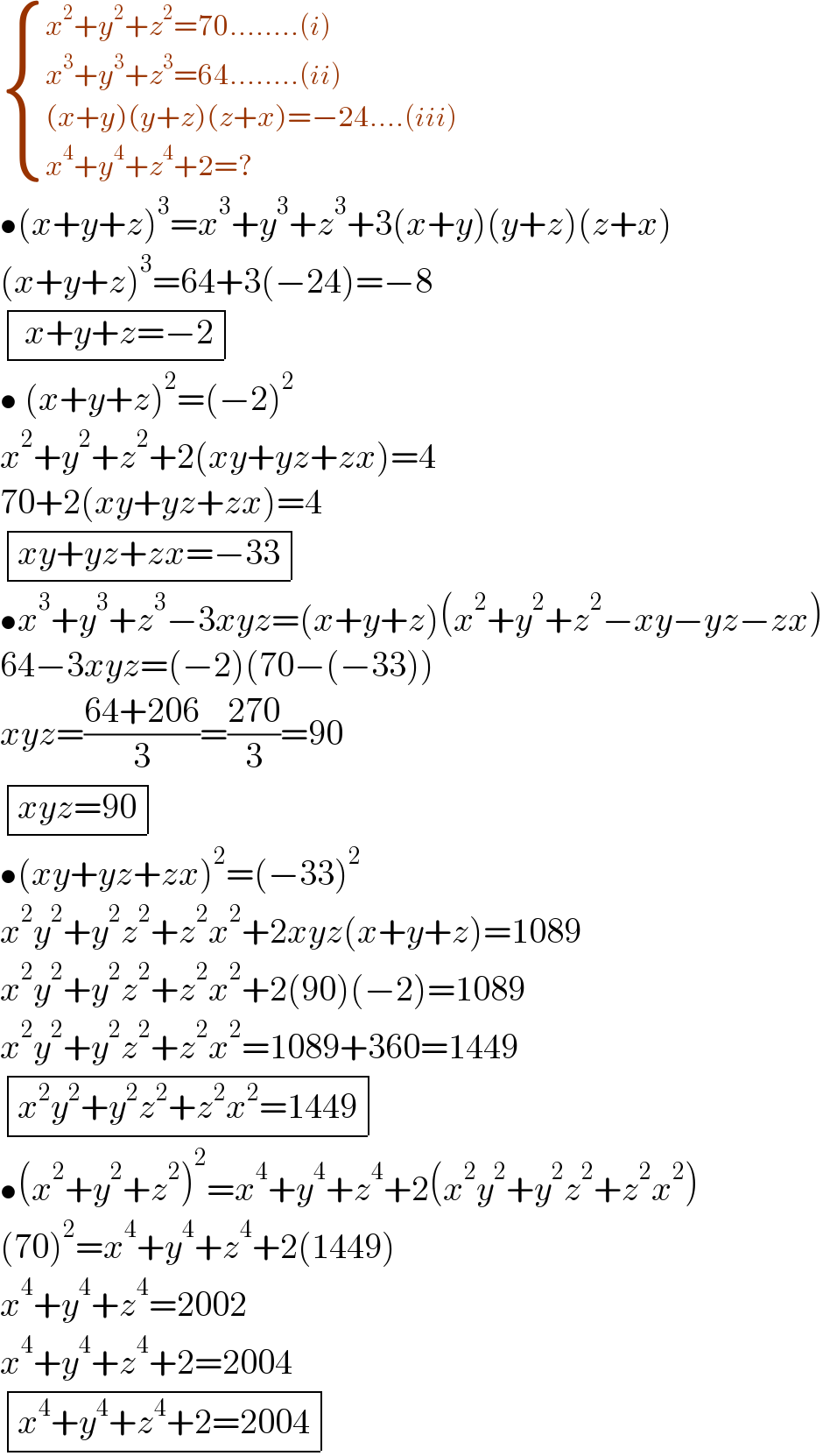
$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{70}……..\left({i}\right)}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{64}……..\left({ii}\right)}\\{\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right)=−\mathrm{24}….\left({iii}\right)}\\{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{2}=?}\end{cases} \\ $$$$\bullet\left({x}+{y}+{z}\right)^{\mathrm{3}} ={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} +\mathrm{3}\left({x}+{y}\right)\left({y}+{z}\right)\left({z}+{x}\right) \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{3}} =\mathrm{64}+\mathrm{3}\left(−\mathrm{24}\right)=−\mathrm{8} \\ $$$$\begin{array}{|c|}{\:{x}+{y}+{z}=−\mathrm{2}}\\\hline\end{array} \\ $$$$\bullet\:\left({x}+{y}+{z}\right)^{\mathrm{2}} =\left(−\mathrm{2}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}\left({xy}+{yz}+{zx}\right)=\mathrm{4} \\ $$$$\mathrm{70}+\mathrm{2}\left({xy}+{yz}+{zx}\right)=\mathrm{4} \\ $$$$\begin{array}{|c|}{{xy}+{yz}+{zx}=−\mathrm{33}}\\\hline\end{array} \\ $$$$\bullet{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{xyz}=\left({x}+{y}+{z}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right) \\ $$$$\mathrm{64}−\mathrm{3}{xyz}=\left(−\mathrm{2}\right)\left(\mathrm{70}−\left(−\mathrm{33}\right)\right) \\ $$$${xyz}=\frac{\mathrm{64}+\mathrm{206}}{\mathrm{3}}=\frac{\mathrm{270}}{\mathrm{3}}=\mathrm{90} \\ $$$$\begin{array}{|c|}{{xyz}=\mathrm{90}}\\\hline\end{array} \\ $$$$\bullet\left({xy}+{yz}+{zx}\right)^{\mathrm{2}} =\left(−\mathrm{33}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{xyz}\left({x}+{y}+{z}\right)=\mathrm{1089} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{90}\right)\left(−\mathrm{2}\right)=\mathrm{1089} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{1089}+\mathrm{360}=\mathrm{1449} \\ $$$$\begin{array}{|c|}{{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{1449}}\\\hline\end{array} \\ $$$$\bullet\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{2}} ={x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{2}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} \right) \\ $$$$\left(\mathrm{70}\right)^{\mathrm{2}} ={x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{2}\left(\mathrm{1449}\right) \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{2002} \\ $$$${x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{2}=\mathrm{2004} \\ $$$$\begin{array}{|c|}{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{2}=\mathrm{2004}}\\\hline\end{array} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Feb/22

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{for}\:\mathrm{rapid}\:\mathrm{feedback}\:\mathrm{sir}! \\ $$$$\left(\mathrm{Here}\:\mathrm{some}\:\mathrm{persons}\:\mathrm{even}\:\mathrm{don}'\mathrm{t}\:\mathrm{give}\right. \\ $$$$\left.\mathrm{any}\:\mathrm{feedback}.\right) \\ $$
Commented by nurtani last updated on 11/Feb/22
$${Nice},\:{Thank}\:{you}\:{sir} \\ $$
