Question-166058

Question Number 166058 by cortano1 last updated on 12/Feb/22

Answered by som(math1967) last updated on 12/Feb/22

△ABC∼△ALB∼△CLB let ∡BAC=∡DCL=α AL×AC=a^2 AL=(a^2 /( (√(a^2 +b^2 )))) LC×AC=b^2 LC=(b^2 /( (√(a^2 +b^2 )))) from△ALB cosα=(a^2 /( (√(a^2 +b^2 ))×a))=(a/( (√(a^2 +b^2 )))) from △LCD cosα=((LC^2 +a^2 −x^2 )/(2LCa)) (a/( (√(a^2 +b^2 ))))=(((b^4 /(a^2 +b^2 ))+a^2 −x^2 )/((2b^2 a)/( (√(a^2 +b^2 ))))) ((2a^2 b^2 )/(a^2 +b^2 ))=((b^4 +a^4 +a^2 b^2 )/(a^2 +b^2 )) −x^2 x^2 =((a^4 −a^2 b^2 +b^4 )/(a^2 +b^2 ))=(((a^2 +b^2 )(a^4 −a^2 b^2 +b^4 ))/((a^2 +b^2 )^2 )) x^2 =(((a^6 +b^6 ))/((a^2 +b^2 )^2 )) ∴ x=((√(a^6 +b^6 ))/(a^2 +b^2 ))

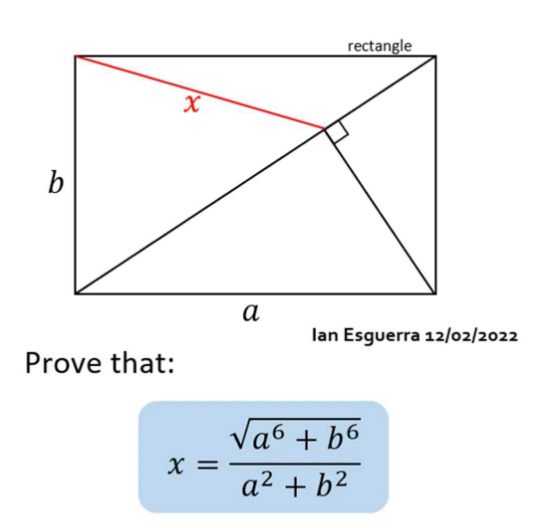
$$\bigtriangleup{ABC}\sim\bigtriangleup{ALB}\sim\bigtriangleup{CLB} \\ $$$${let}\:\measuredangle{BAC}=\measuredangle{DCL}=\alpha \\ $$$${AL}×{AC}={a}^{\mathrm{2}} \\ $$$${AL}=\frac{{a}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${LC}×{AC}={b}^{\mathrm{2}} \\ $$$${LC}=\frac{{b}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${from}\bigtriangleup{ALB}\:{cos}\alpha=\frac{{a}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }×{a}}=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${from}\:\bigtriangleup{LCD}\: \\ $$$${cos}\alpha=\frac{{LC}^{\mathrm{2}} +{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\mathrm{2}{LCa}} \\ $$$$\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}=\frac{\frac{{b}^{\mathrm{4}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\frac{\mathrm{2}{b}^{\mathrm{2}} {a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}} \\ $$$$\frac{\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\frac{{b}^{\mathrm{4}} +{a}^{\mathrm{4}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:−{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\frac{{a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} \right)}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} =\frac{\left({a}^{\mathrm{6}} +{b}^{\mathrm{6}} \right)}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\therefore\:\boldsymbol{{x}}=\frac{\sqrt{\boldsymbol{{a}}^{\mathrm{6}} +\boldsymbol{{b}}^{\mathrm{6}} }}{\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} } \\ $$

Commented by som(math1967) last updated on 12/Feb/22

Commented by Tawa11 last updated on 12/Feb/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply