Question Number 166111 by DAVONG last updated on 13/Feb/22
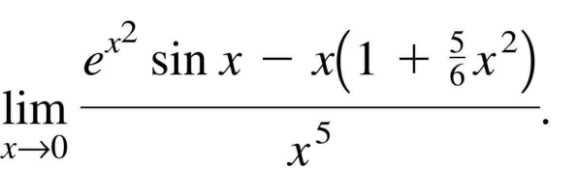
Answered by qaz last updated on 13/Feb/22
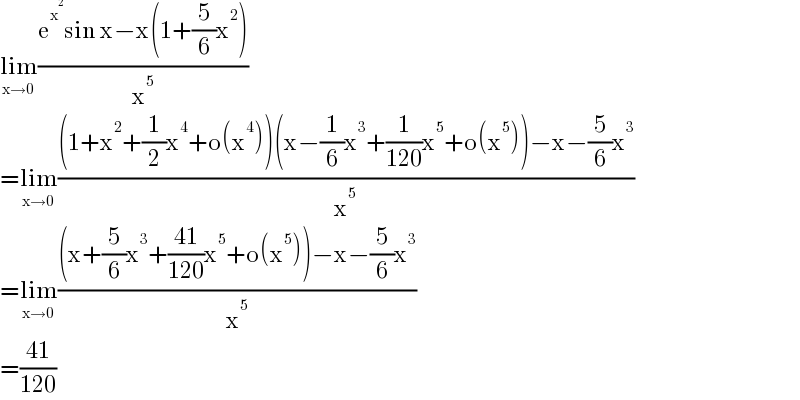
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \mathrm{sin}\:\mathrm{x}−\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{4}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)\right)\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{120}}\mathrm{x}^{\mathrm{5}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)−\mathrm{x}−\frac{\mathrm{5}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}+\frac{\mathrm{5}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{41}}{\mathrm{120}}\mathrm{x}^{\mathrm{5}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)−\mathrm{x}−\frac{\mathrm{5}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{41}}{\mathrm{120}} \\ $$
