Question-166137

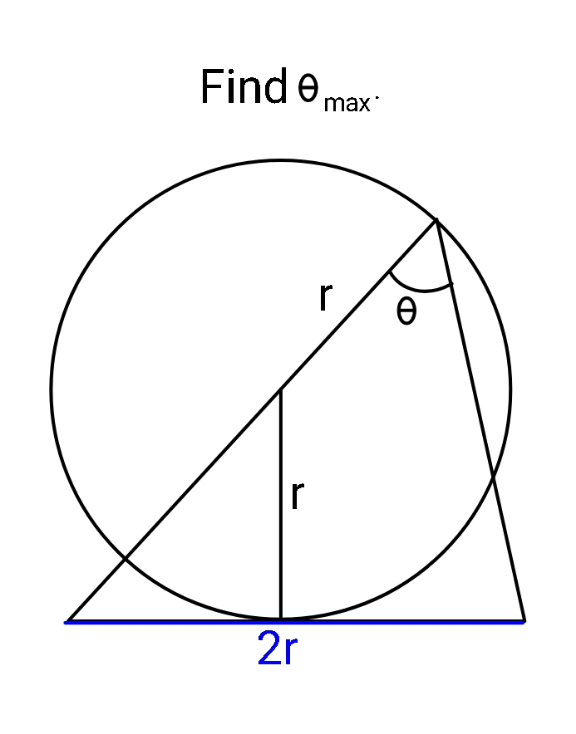
Question Number 166137 by ajfour last updated on 13/Feb/22

Answered by mr W last updated on 14/Feb/22

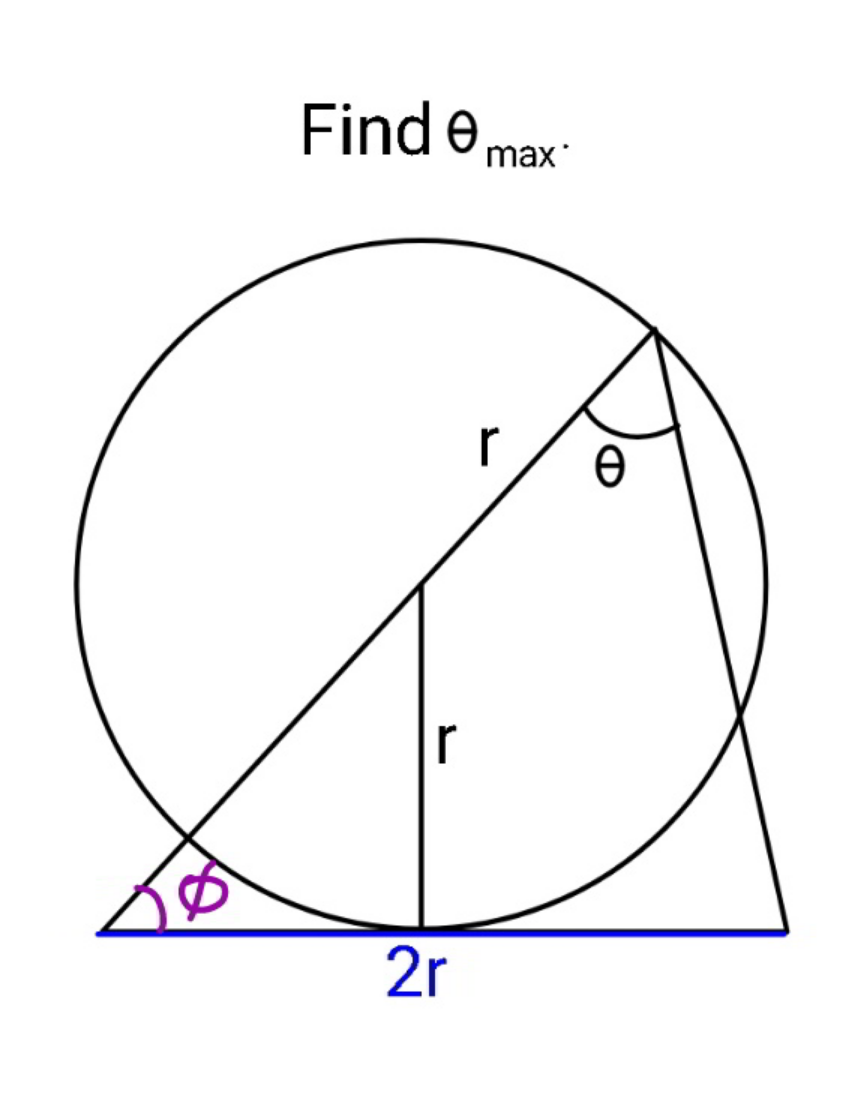
Commented by mr W last updated on 14/Feb/22

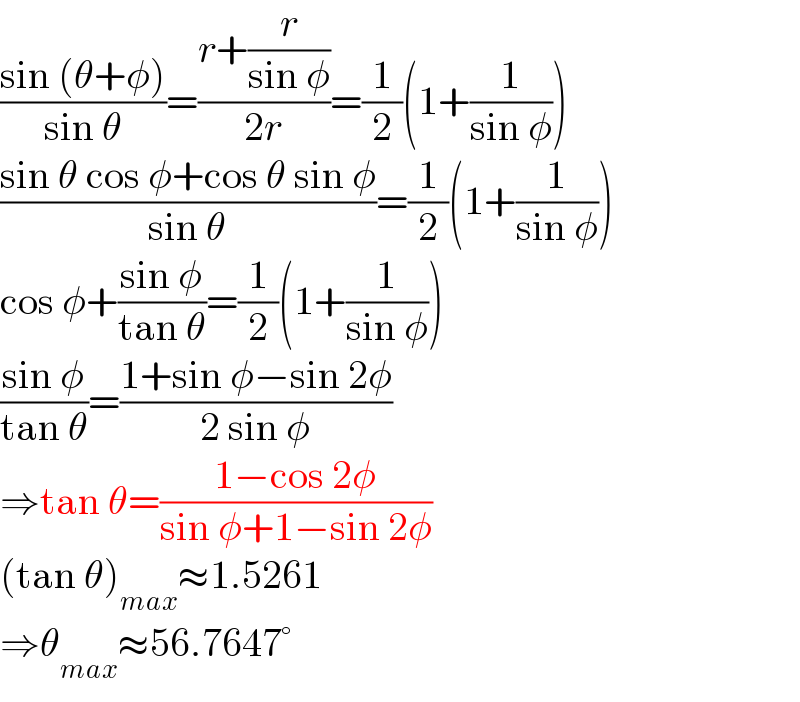
((sin (θ+φ))/(sin θ))=((r+(r/(sin φ)))/(2r))=(1/2)(1+(1/(sin φ))) ((sin θ cos φ+cos θ sin φ)/(sin θ))=(1/2)(1+(1/(sin φ))) cos φ+((sin φ)/(tan θ))=(1/2)(1+(1/(sin φ))) ((sin φ)/(tan θ))=((1+sin φ−sin 2φ)/(2 sin φ)) ⇒tan θ=((1−cos 2φ)/(sin φ+1−sin 2φ)) (tan θ)_(max) ≈1.5261 ⇒θ_(max) ≈56.7647°

$$\frac{\mathrm{sin}\:\left(\theta+\phi\right)}{\mathrm{sin}\:\theta}=\frac{{r}+\frac{{r}}{\mathrm{sin}\:\phi}}{\mathrm{2}{r}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sin}\:\phi}\right) \\ $$$$\frac{\mathrm{sin}\:\theta\:\mathrm{cos}\:\phi+\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sin}\:\phi}\right) \\ $$$$\mathrm{cos}\:\phi+\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sin}\:\phi}\right) \\ $$$$\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}=\frac{\mathrm{1}+\mathrm{sin}\:\phi−\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{2}\:\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\phi}{\mathrm{sin}\:\phi+\mathrm{1}−\mathrm{sin}\:\mathrm{2}\phi} \\ $$$$\left(\mathrm{tan}\:\theta\right)_{{max}} \approx\mathrm{1}.\mathrm{5261} \\ $$$$\Rightarrow\theta_{{max}} \approx\mathrm{56}.\mathrm{7647}° \\ $$

Answered by MJS_new last updated on 14/Feb/22

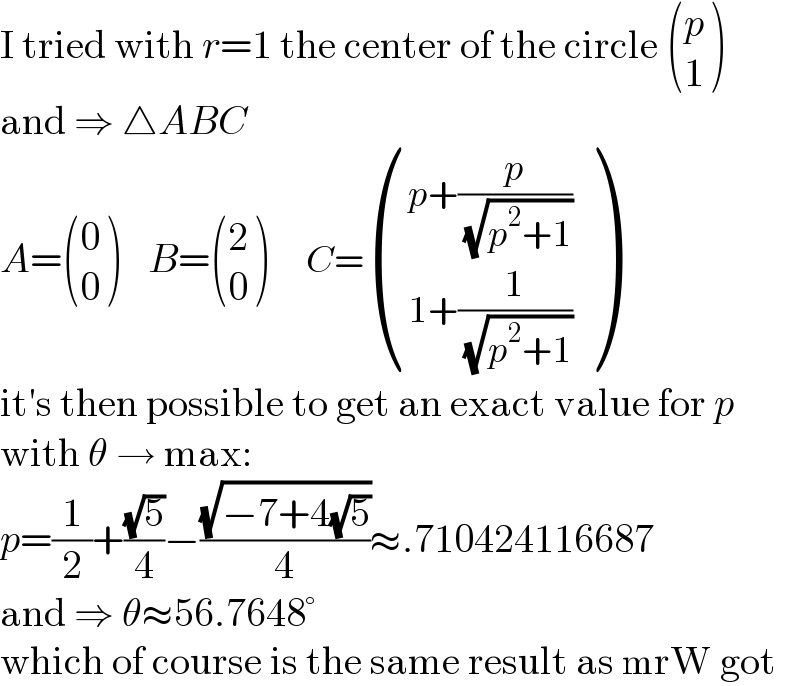
I tried with r=1 the center of the circle ((p),(1) ) and ⇒ △ABC A= ((0),(0) ) B= ((2),(0) ) C= (((p+(p/( (√(p^2 +1)))))),((1+(1/( (√(p^2 +1)))))) ) it′s then possible to get an exact value for p with θ → max: p=(1/2)+((√5)/4)−((√(−7+4(√5)))/4)≈.710424116687 and ⇒ θ≈56.7648° which of course is the same result as mrW got

$$\mathrm{I}\:\mathrm{tried}\:\mathrm{with}\:{r}=\mathrm{1}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\begin{pmatrix}{{p}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{and}\:\Rightarrow\:\bigtriangleup{ABC} \\ $$$${A}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\:\:\:\:{B}=\begin{pmatrix}{\mathrm{2}}\\{\mathrm{0}}\end{pmatrix}\:\:\:\:\:{C}=\begin{pmatrix}{{p}+\frac{{p}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}}\\{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}}}\end{pmatrix} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{then}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{get}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{for}\:{p} \\ $$$$\mathrm{with}\:\theta\:\rightarrow\:\mathrm{max}: \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}−\frac{\sqrt{−\mathrm{7}+\mathrm{4}\sqrt{\mathrm{5}}}}{\mathrm{4}}\approx.\mathrm{710424116687} \\ $$$$\mathrm{and}\:\Rightarrow\:\theta\approx\mathrm{56}.\mathrm{7648}° \\ $$$$\mathrm{which}\:\mathrm{of}\:\mathrm{course}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}\:\mathrm{as}\:\mathrm{mrW}\:\mathrm{got} \\ $$

Commented by mr W last updated on 15/Feb/22

$${great}\:{sir}! \\ $$$${somehow}\:{i}\:{have}\:{expected}\:{that}\:{you} \\ $$$${may}\:{get}\:{the}\:{exact}\:{solution}.\:{thanks}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply