Question Number 166195 by mathlove last updated on 15/Feb/22

Answered by alephzero last updated on 15/Feb/22

$${x}\:=\:\mathrm{1} \\ $$
Commented by mathlove last updated on 15/Feb/22

$${how}? \\ $$
Commented by alephzero last updated on 15/Feb/22

$$ \\ $$$$ \\ $$
Commented by alephzero last updated on 15/Feb/22
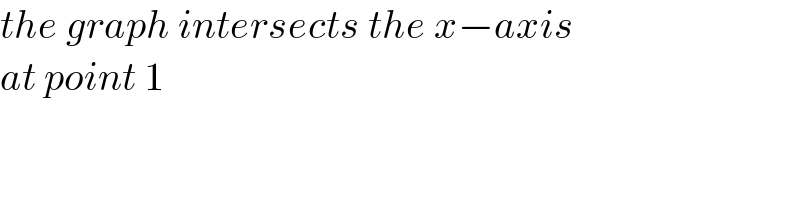
$${the}\:{graph}\:{intersects}\:{the}\:{x}−{axis} \\ $$$${at}\:{point}\:\mathrm{1} \\ $$
Commented by mr W last updated on 15/Feb/22
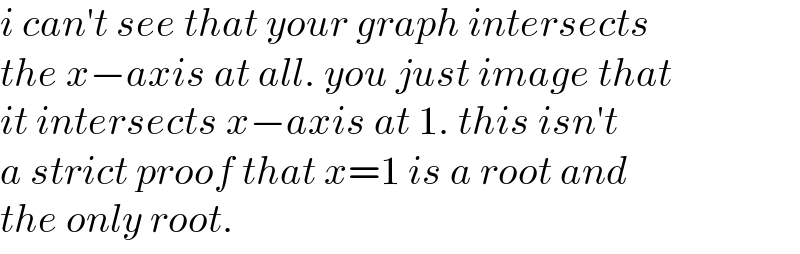
$${i}\:{can}'{t}\:{see}\:{that}\:{your}\:{graph}\:{intersects} \\ $$$${the}\:{x}−{axis}\:{at}\:{all}.\:{you}\:{just}\:{image}\:{that} \\ $$$${it}\:{intersects}\:{x}−{axis}\:{at}\:\mathrm{1}.\:{this}\:{isn}'{t} \\ $$$${a}\:{strict}\:{proof}\:{that}\:{x}=\mathrm{1}\:{is}\:{a}\:{root}\:{and} \\ $$$${the}\:{only}\:{root}. \\ $$
Answered by mathsmine last updated on 15/Feb/22
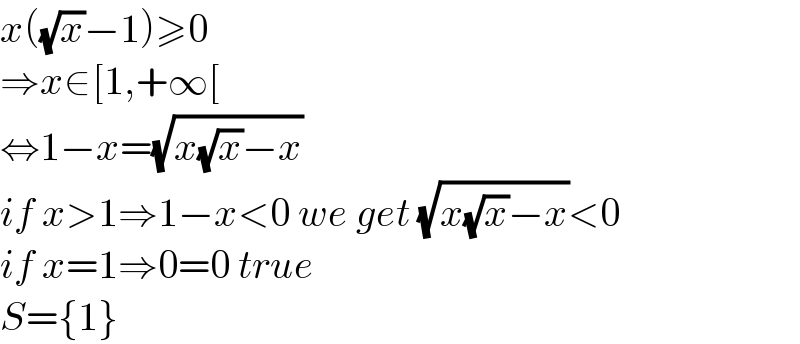
$${x}\left(\sqrt{{x}}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\in\left[\mathrm{1},+\infty\left[\right.\right. \\ $$$$\Leftrightarrow\mathrm{1}−{x}=\sqrt{{x}\sqrt{{x}}−{x}} \\ $$$${if}\:{x}>\mathrm{1}\Rightarrow\mathrm{1}−{x}<\mathrm{0}\:{we}\:{get}\:\sqrt{{x}\sqrt{{x}}−{x}}<\mathrm{0} \\ $$$${if}\:{x}=\mathrm{1}\Rightarrow\mathrm{0}=\mathrm{0}\:{true}\: \\ $$$${S}=\left\{\mathrm{1}\right\} \\ $$
Answered by TheSupreme last updated on 15/Feb/22
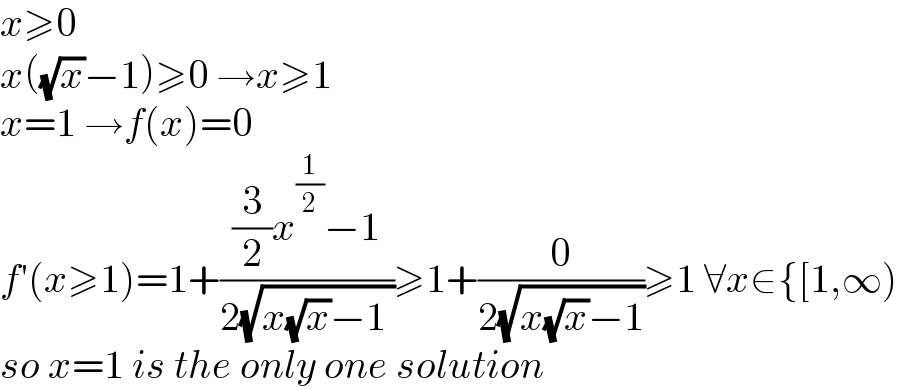
$${x}\geqslant\mathrm{0} \\ $$$${x}\left(\sqrt{{x}}−\mathrm{1}\right)\geqslant\mathrm{0}\:\rightarrow{x}\geqslant\mathrm{1} \\ $$$${x}=\mathrm{1}\:\rightarrow{f}\left({x}\right)=\mathrm{0} \\ $$$${f}'\left({x}\geqslant\mathrm{1}\right)=\mathrm{1}+\frac{\frac{\mathrm{3}}{\mathrm{2}}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}}{\mathrm{2}\sqrt{{x}\sqrt{{x}}−\mathrm{1}\:}}\geqslant\mathrm{1}+\frac{\mathrm{0}}{\mathrm{2}\sqrt{{x}\sqrt{{x}}−\mathrm{1}}}\geqslant\mathrm{1}\:\forall{x}\in\left\{\left[\mathrm{1},\infty\right)\right. \\ $$$${so}\:{x}=\mathrm{1}\:{is}\:{the}\:{only}\:{one}\:{solution} \\ $$
