Question Number 166215 by mathlove last updated on 15/Feb/22

Answered by nurtani last updated on 15/Feb/22
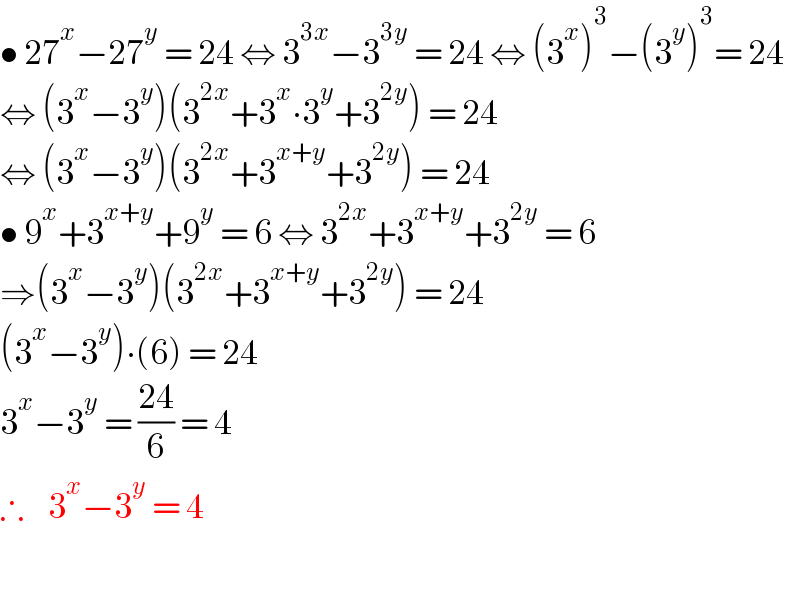
$$\bullet\:\mathrm{27}^{{x}} −\mathrm{27}^{{y}} \:=\:\mathrm{24}\:\Leftrightarrow\:\mathrm{3}^{\mathrm{3}{x}} −\mathrm{3}^{\mathrm{3}{y}} \:=\:\mathrm{24}\:\Leftrightarrow\:\left(\mathrm{3}^{{x}} \right)^{\mathrm{3}} −\left(\mathrm{3}^{{y}} \right)^{\mathrm{3}} =\:\mathrm{24} \\ $$$$\Leftrightarrow\:\left(\mathrm{3}^{{x}} −\mathrm{3}^{{y}} \right)\left(\mathrm{3}^{\mathrm{2}{x}} +\mathrm{3}^{{x}} \centerdot\mathrm{3}^{{y}} +\mathrm{3}^{\mathrm{2}{y}} \right)\:=\:\mathrm{24} \\ $$$$\Leftrightarrow\:\left(\mathrm{3}^{{x}} −\mathrm{3}^{{y}} \right)\left(\mathrm{3}^{\mathrm{2}{x}} +\mathrm{3}^{{x}+{y}} +\mathrm{3}^{\mathrm{2}{y}} \right)\:=\:\mathrm{24} \\ $$$$\bullet\:\mathrm{9}^{{x}} +\mathrm{3}^{{x}+{y}} +\mathrm{9}^{{y}} \:=\:\mathrm{6}\:\Leftrightarrow\:\mathrm{3}^{\mathrm{2}{x}} +\mathrm{3}^{{x}+{y}} +\mathrm{3}^{\mathrm{2}{y}} \:=\:\mathrm{6} \\ $$$$\Rightarrow\left(\mathrm{3}^{{x}} −\mathrm{3}^{{y}} \right)\left(\mathrm{3}^{\mathrm{2}{x}} +\mathrm{3}^{{x}+{y}} +\mathrm{3}^{\mathrm{2}{y}} \right)\:=\:\mathrm{24} \\ $$$$\left(\mathrm{3}^{{x}} −\mathrm{3}^{{y}} \right)\centerdot\left(\mathrm{6}\right)\:=\:\mathrm{24} \\ $$$$\mathrm{3}^{{x}} −\mathrm{3}^{{y}} \:=\:\frac{\mathrm{24}}{\mathrm{6}}\:=\:\mathrm{4} \\ $$$$\therefore\:\:\:\:\mathrm{3}^{{x}} −\mathrm{3}^{{y}} \:=\:\mathrm{4} \\ $$$$\: \\ $$
