Question Number 166252 by mr W last updated on 16/Feb/22
Commented by mr W last updated on 16/Feb/22
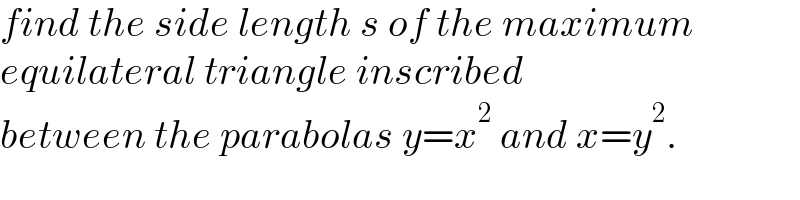
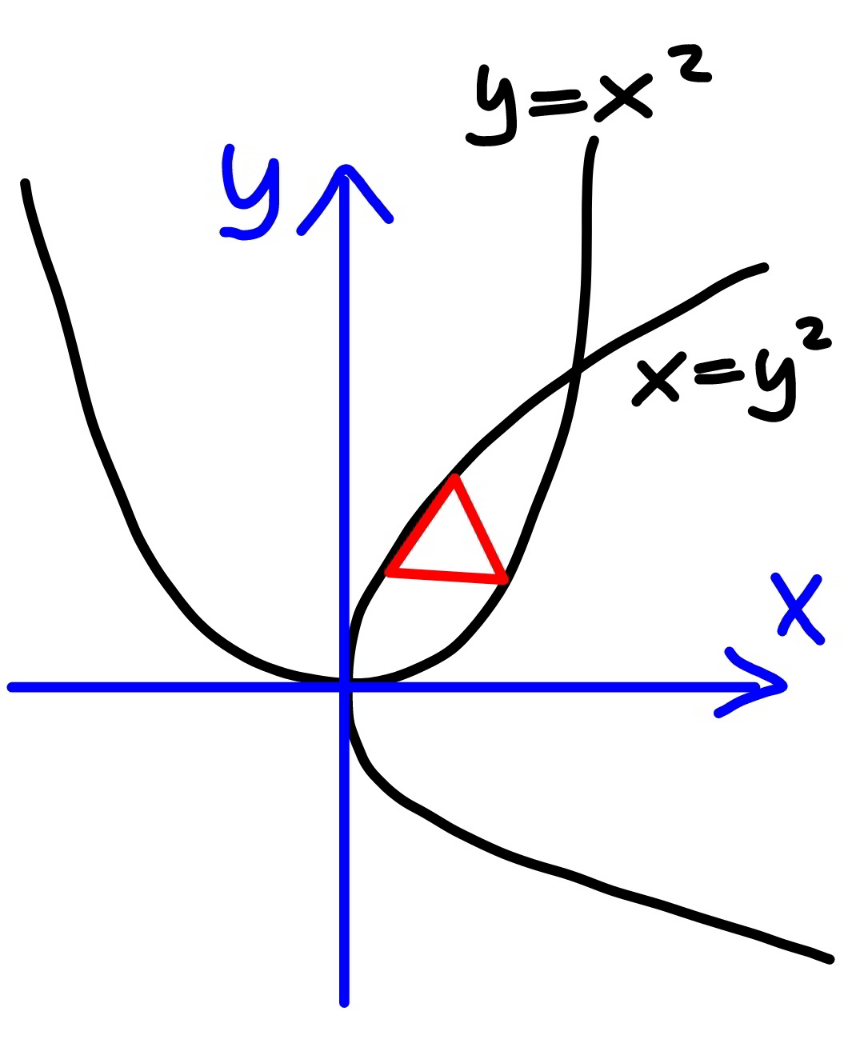
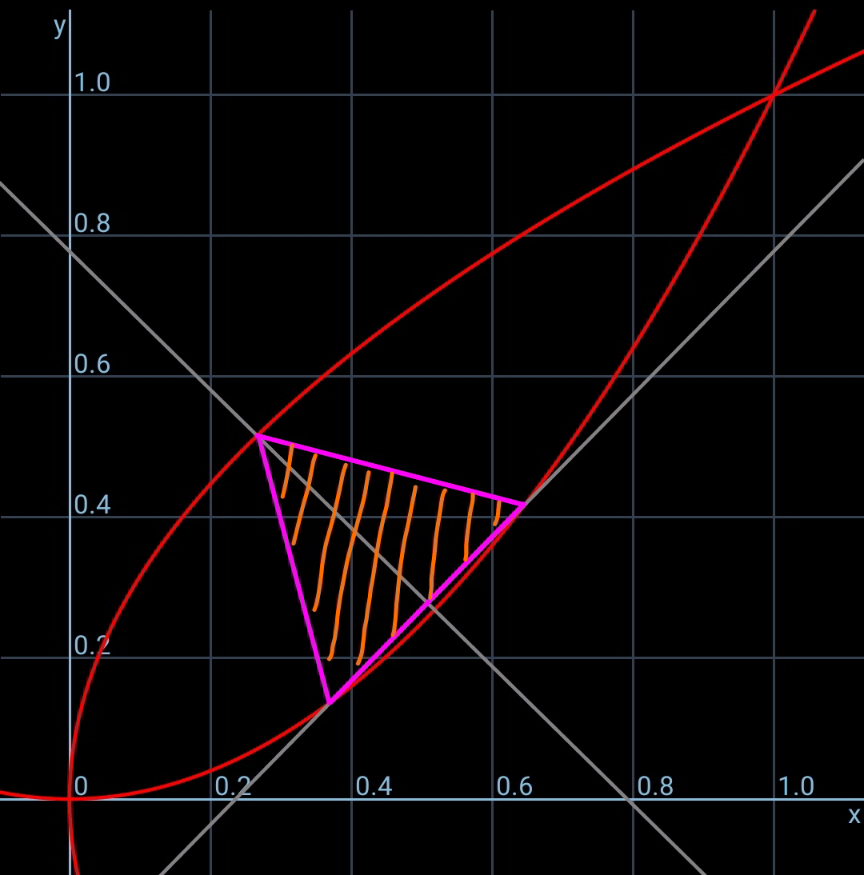
$${find}\:{the}\:{side}\:{length}\:{s}\:{of}\:{the}\:{maximum} \\ $$$${equilateral}\:{triangle}\:{inscribed} \\ $$$${between}\:{the}\:{parabolas}\:{y}={x}^{\mathrm{2}} \:{and}\:{x}={y}^{\mathrm{2}} . \\ $$
Answered by mr W last updated on 18/Feb/22
Commented by mr W last updated on 19/Feb/22
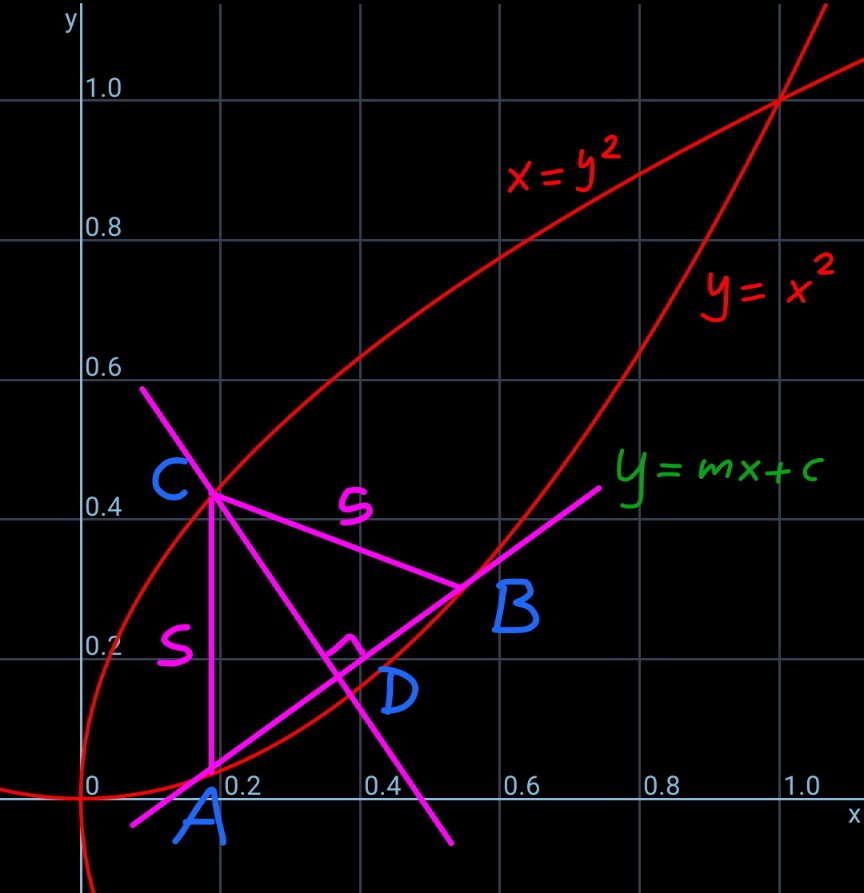
![say eqn. of AB is y=mx+c x^2 −mx−c=0 x_A +x_B =m x_A x_B =−c s^2 =(x_B −x_A )^2 +(y_B −y_A )^2 s^2 =(x_B −x_A )^2 +(x_B −x_A )^2 (x_B +x_A )^2 s^2 =(x_B −x_A )^2 [1+(x_B +x_A )^2 ] s^2 =Φ=(m^2 +4c)(1+m^2 ) ⇒c=(Φ/(4(1+m^2 )))−(m^2 /4) ✓ x_D =((x_A +x_B )/2)=(m/2) y_D =((y_A +y_B )/2)=((x_A ^2 +x_B ^2 )/2)=(((x_A +x_B )^2 −2x_A x_B )/2) y_D =(m^2 /2)+c eqn. of DC: y=y_D −(1/m)(x−x_D ) y=(m^2 /2)+c−(1/m)(x−(m/2)) y=((1+m^2 )/2)+c−(x/m) y^2 +my−((m(1+m^2 ))/2)−mc=0 y_C =((−m+(√(m(2m^2 +m+2+4c))))/2) mx_C −y_C +c=(1+m^2 )((m^2 /2)+c−y_C ) mx_C −y_C +c=(1+m^2 )(((m^2 +m)/2)+c−((√(m(2m^2 +m+2+4c)))/2)) CD=(((√3)s)/2) ((3s^2 )/4)=(((mx_C −y_C +c)^2 )/(1+m^2 )) 3Φ=(1+m^2 )[m^2 +m+2c−(√(m(2m^2 +m+2+4c)))]^2 Φ_(max) ≈0.1541 at m≈1.018 s_(max) ≈0.3926](https://www.tinkutara.com/question/Q166344.png)
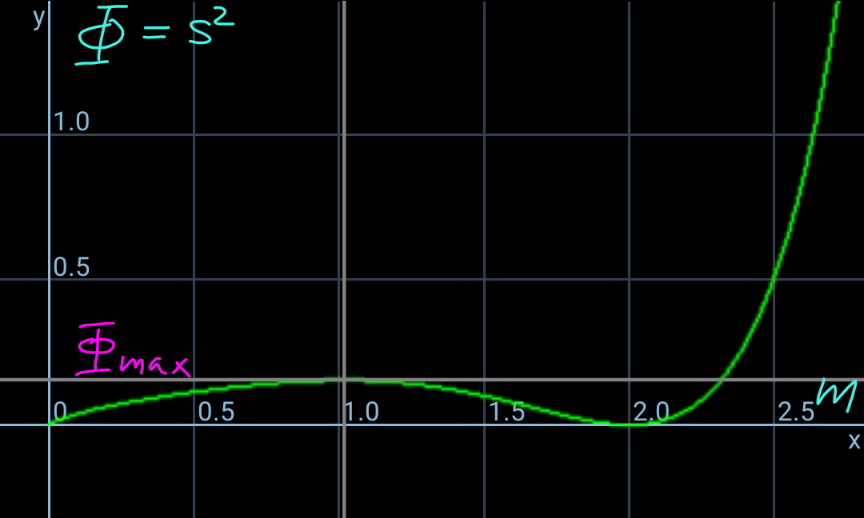
$${say}\:{eqn}.\:{of}\:{AB}\:{is}\:{y}={mx}+{c} \\ $$$${x}^{\mathrm{2}} −{mx}−{c}=\mathrm{0} \\ $$$${x}_{{A}} +{x}_{{B}} ={m} \\ $$$${x}_{{A}} {x}_{{B}} =−{c} \\ $$$${s}^{\mathrm{2}} =\left({x}_{{B}} −{x}_{{A}} \right)^{\mathrm{2}} +\left({y}_{{B}} −{y}_{{A}} \right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({x}_{{B}} −{x}_{{A}} \right)^{\mathrm{2}} +\left({x}_{{B}} −{x}_{{A}} \right)^{\mathrm{2}} \left({x}_{{B}} +{x}_{{A}} \right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({x}_{{B}} −{x}_{{A}} \right)^{\mathrm{2}} \left[\mathrm{1}+\left({x}_{{B}} +{x}_{{A}} \right)^{\mathrm{2}} \right] \\ $$$${s}^{\mathrm{2}} =\Phi=\left({m}^{\mathrm{2}} +\mathrm{4}{c}\right)\left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{c}=\frac{\Phi}{\mathrm{4}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}−\frac{{m}^{\mathrm{2}} }{\mathrm{4}}\:\checkmark \\ $$$${x}_{{D}} =\frac{{x}_{{A}} +{x}_{{B}} }{\mathrm{2}}=\frac{{m}}{\mathrm{2}} \\ $$$${y}_{{D}} =\frac{{y}_{{A}} +{y}_{{B}} }{\mathrm{2}}=\frac{{x}_{{A}} ^{\mathrm{2}} +{x}_{{B}} ^{\mathrm{2}} }{\mathrm{2}}=\frac{\left({x}_{{A}} +{x}_{{B}} \right)^{\mathrm{2}} −\mathrm{2}{x}_{{A}} {x}_{{B}} }{\mathrm{2}} \\ $$$${y}_{{D}} =\frac{{m}^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$${eqn}.\:{of}\:{DC}: \\ $$$${y}={y}_{{D}} −\frac{\mathrm{1}}{{m}}\left({x}−{x}_{{D}} \right) \\ $$$${y}=\frac{{m}^{\mathrm{2}} }{\mathrm{2}}+{c}−\frac{\mathrm{1}}{{m}}\left({x}−\frac{{m}}{\mathrm{2}}\right) \\ $$$${y}=\frac{\mathrm{1}+{m}^{\mathrm{2}} }{\mathrm{2}}+{c}−\frac{{x}}{{m}} \\ $$$${y}^{\mathrm{2}} +{my}−\frac{{m}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{2}}−{mc}=\mathrm{0} \\ $$$${y}_{{C}} =\frac{−{m}+\sqrt{{m}\left(\mathrm{2}{m}^{\mathrm{2}} +{m}+\mathrm{2}+\mathrm{4}{c}\right)}}{\mathrm{2}} \\ $$$${mx}_{{C}} −{y}_{{C}} +{c}=\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\frac{{m}^{\mathrm{2}} }{\mathrm{2}}+{c}−{y}_{{C}} \right) \\ $$$${mx}_{{C}} −{y}_{{C}} +{c}=\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\frac{{m}^{\mathrm{2}} +{m}}{\mathrm{2}}+{c}−\frac{\sqrt{{m}\left(\mathrm{2}{m}^{\mathrm{2}} +{m}+\mathrm{2}+\mathrm{4}{c}\right)}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${CD}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{4}}=\frac{\left({mx}_{{C}} −{y}_{{C}} +{c}\right)^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\mathrm{3}\Phi=\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left[{m}^{\mathrm{2}} +{m}+\mathrm{2}{c}−\sqrt{{m}\left(\mathrm{2}{m}^{\mathrm{2}} +{m}+\mathrm{2}+\mathrm{4}{c}\right)}\right]^{\mathrm{2}} \\ $$$$\Phi_{{max}} \approx\mathrm{0}.\mathrm{1541}\:{at}\:{m}\approx\mathrm{1}.\mathrm{018} \\ $$$${s}_{{max}} \approx\mathrm{0}.\mathrm{3926} \\ $$
Commented by mr W last updated on 19/Feb/22
Commented by mr W last updated on 19/Feb/22
Commented by ajfour last updated on 19/Feb/22
![A(p,p^2 ) C[p+scos (θ+60°), p^2 +ssin (θ+60°)] B[p+scos θ, p^2 +ssin θ] p^2 +ssin θ=(p+scos θ)^2 ⇒ sin θ−2pcos θ=scos^2 θ ⇒ 2p=tan θ−scos θ & p+scos (θ+60°) ={p^2 +ssin (θ+60°)}^2 ⇒ 8(tan θ−scos θ)+16scos (θ+60°) ={(tan θ−scos θ)^2 +4ssin (θ+60°)}^2 s_(max) ≈ 0.39254](https://www.tinkutara.com/question/Q166413.png)
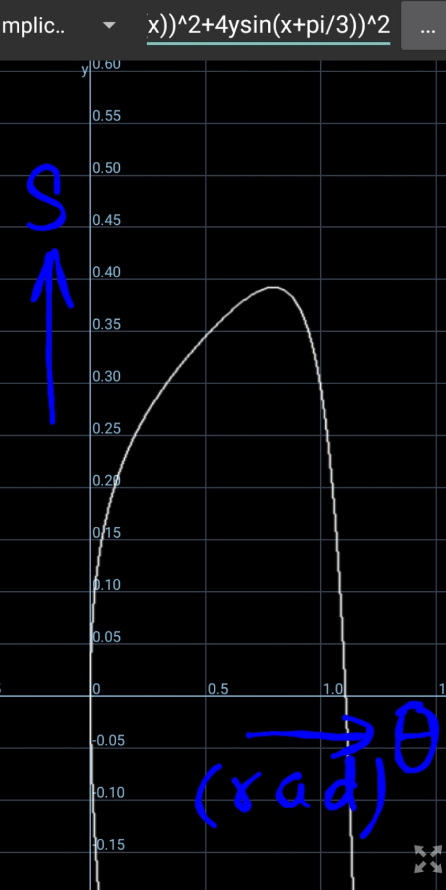
$${A}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${C}\left[{p}+{s}\mathrm{cos}\:\left(\theta+\mathrm{60}°\right),\:{p}^{\mathrm{2}} +{s}\mathrm{sin}\:\left(\theta+\mathrm{60}°\right)\right] \\ $$$${B}\left[{p}+{s}\mathrm{cos}\:\theta,\:{p}^{\mathrm{2}} +{s}\mathrm{sin}\:\theta\right] \\ $$$${p}^{\mathrm{2}} +{s}\mathrm{sin}\:\theta=\left({p}+{s}\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\theta−\mathrm{2}{p}\mathrm{cos}\:\theta={s}\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$\Rightarrow\:\:\mathrm{2}{p}=\mathrm{tan}\:\theta−{s}\mathrm{cos}\:\theta \\ $$$$\&\:\:{p}+{s}\mathrm{cos}\:\left(\theta+\mathrm{60}°\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left\{{p}^{\mathrm{2}} +{s}\mathrm{sin}\:\left(\theta+\mathrm{60}°\right)\right\}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{8}\left(\mathrm{tan}\:\theta−{s}\mathrm{cos}\:\theta\right)+\mathrm{16}{s}\mathrm{cos}\:\left(\theta+\mathrm{60}°\right) \\ $$$$\:\:=\left\{\left(\mathrm{tan}\:\theta−{s}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mathrm{4}{s}\mathrm{sin}\:\left(\theta+\mathrm{60}°\right)\right\}^{\mathrm{2}} \\ $$$$\:\:{s}_{{max}} \approx\:\mathrm{0}.\mathrm{39254}\:\: \\ $$
Commented by ajfour last updated on 19/Feb/22
Commented by mr W last updated on 19/Feb/22
$${nice}\:{solution}!\:{thanks}\:{sir}! \\ $$
