Question Number 166350 by mkam last updated on 18/Feb/22

Commented by mkam last updated on 18/Feb/22

$${how}\:{can}\:{it}\:{solve}\:{this}\:{proplem}\:{it}\:{is}\:{very}\:{hard}\:{helps}\:{me}\:? \\ $$
Answered by mahdipoor last updated on 18/Feb/22
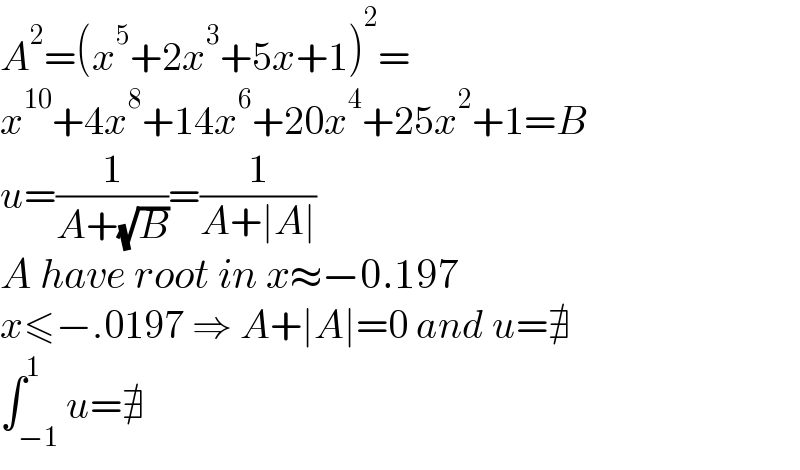
$${A}^{\mathrm{2}} =\left({x}^{\mathrm{5}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{5}{x}+\mathrm{1}\right)^{\mathrm{2}} = \\ $$$${x}^{\mathrm{10}} +\mathrm{4}{x}^{\mathrm{8}} +\mathrm{14}{x}^{\mathrm{6}} +\mathrm{20}{x}^{\mathrm{4}} +\mathrm{25}{x}^{\mathrm{2}} +\mathrm{1}={B} \\ $$$${u}=\frac{\mathrm{1}}{{A}+\sqrt{{B}}}=\frac{\mathrm{1}}{{A}+\mid{A}\mid} \\ $$$${A}\:{have}\:{root}\:{in}\:{x}\approx−\mathrm{0}.\mathrm{197} \\ $$$${x}\leqslant−.\mathrm{0197}\:\Rightarrow\:{A}+\mid{A}\mid=\mathrm{0}\:{and}\:{u}=\nexists \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{1}} {u}=\nexists \\ $$
