Question Number 166417 by ajfour last updated on 19/Feb/22
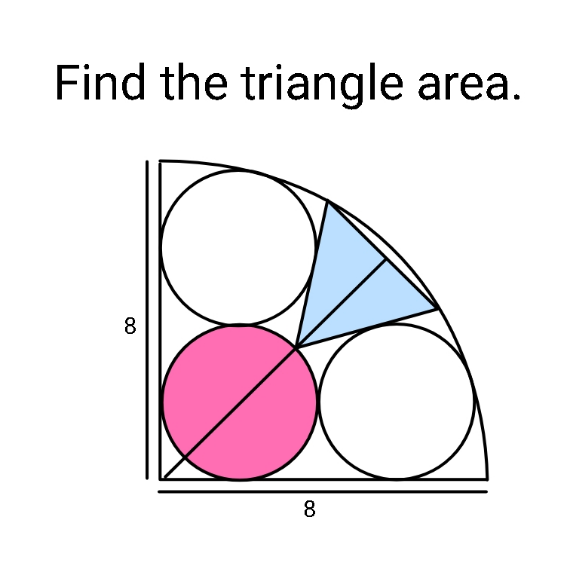
Answered by mr W last updated on 20/Feb/22
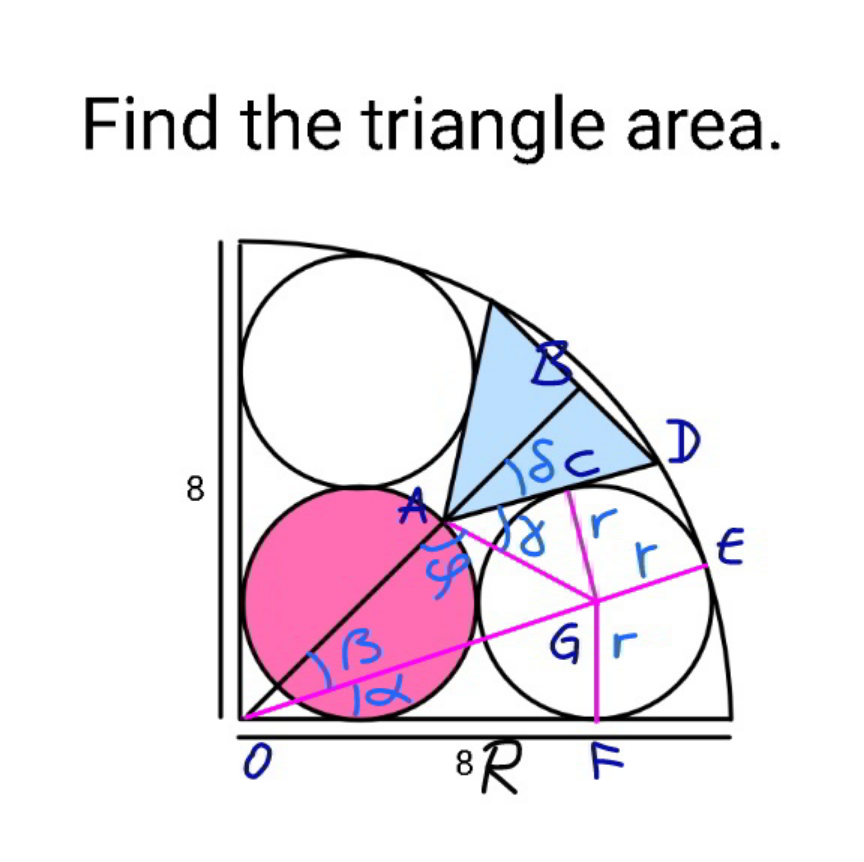
Commented by mr W last updated on 20/Feb/22
![OG=R−r OF=3r (R−r)^2 =(3r)^2 +r^2 9r^2 +2Rr−R^2 =0 ⇒r=((((√(10))−1)R)/9) tan α=(1/3) ⇒α=tan^(−1) (1/3) β=(π/4)−α OA=(1+(√2))r AG^2 =(1+(√2))^2 r^2 +((√(10))r)^2 −2(1+(√2))(√(10))r^2 cos β AG^2 =(13+2(√2)−2(1+(√2))(√(10)) (1/( (√2)))((3/( (√(10))))+(1/( (√(10))))))r^2 AG^2 =(5−2(√2))r^2 AG=(√(5−2(√2)))r ✓ ((sin ϕ)/( (√(10))r))=((sin β)/( (√(5−2(√2)))r)) sin ϕ=((√(10))/( (√(5−2(√2)))))×(1/( (√2)))((3/( (√(10))))−(1/( (√(10))))) sin ϕ=((√2)/( (√(5−2(√2))))) ⇒ϕ=π−sin^(−1) ((√2)/( (√(5−2(√2))))) sin γ=(1/( (√(5−2(√2))))) ⇒γ=sin^(−1) (1/( (√(5−2(√2))))) δ=π−ϕ−γ=sin^(−1) ((√2)/( (√(5−2(√2)))))−sin^(−1) (1/( (√(5−2(√2))))) cos δ=((√((5−2(√2)−2)(5−2(√2)−1)))/(5−2(√2)))+((√2)/(5−2(√2))) cos δ=(((√2)(1+(√(10−7(√2)))))/(5−2(√2))) sin δ=(((√(2(5−2(√2)−1)))−(√(5−2(√2)−2)))/(5−2(√2))) sin δ=((2(√(2−(√2)))+1−(√2))/(5−2(√2))) OB=(1+(√2))r+AD cos δ BD=AD sin δ OB^2 +BD^2 =OD^2 =R^2 [(1+(√2))r+AD cos δ]^2 +(AD sin δ)^2 =R^2 (AD)^2 +2(1+(√2)) cos δ AD+(1+(√2))^2 −R^2 =0 (((AD)/r))^2 +2(1+(√2)) cos δ(((AD)/r))+(1+(√2))^2 −((9/( (√(10))−1)))^2 =0 (((AD)/r))^2 +2(1+(√2))(((√2)(1+(√(10−7(√2)))))/(5−2(√2)))(((AD)/r))+(1+(√2))^2 −((9/( (√(10))−1)))^2 =0 (((AD)/r))^2 +((2(14+9(√2))(1+(√(10−7(√2)))))/(17))(((AD)/r))−2(4+(√(10))−(√2))=0 ((AD)/r)=−(((14+9(√2))(1+(√(10−7(√2)))))/(17))+(√((((14+9(√2))^2 (1+(√(10−7(√2))))^2 )/(17^2 ))+2(4+(√(10))−(√2)))) ((AD)/r)=(((√(2722+578(√(10))−312(√2)+(716+504(√2))(√(10−7(√2)))))−(14+9(√2))(1+(√(10−7(√2)))))/(17)) Area of triangle A=(AD)^2 sin δ cos δ ≈1.5956802 r^2 ≈0.0921051R^2 ≈5.8947276](https://www.tinkutara.com/question/Q166432.png)
$${OG}={R}−{r} \\ $$$${OF}=\mathrm{3}{r} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} =\left(\mathrm{3}{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$\mathrm{9}{r}^{\mathrm{2}} +\mathrm{2}{Rr}−{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{\left(\sqrt{\mathrm{10}}−\mathrm{1}\right){R}}{\mathrm{9}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\beta=\frac{\pi}{\mathrm{4}}−\alpha \\ $$$${OA}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){r} \\ $$$${AG}^{\mathrm{2}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} {r}^{\mathrm{2}} +\left(\sqrt{\mathrm{10}}{r}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{10}}{r}^{\mathrm{2}} \:\mathrm{cos}\:\beta \\ $$$${AG}^{\mathrm{2}} =\left(\mathrm{13}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{10}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\right)\right){r}^{\mathrm{2}} \\ $$$${AG}^{\mathrm{2}} =\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}\right){r}^{\mathrm{2}} \\ $$$${AG}=\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}{r}\:\checkmark \\ $$$$\frac{\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{10}}{r}}=\frac{\mathrm{sin}\:\beta}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}{r}} \\ $$$$\mathrm{sin}\:\varphi=\frac{\sqrt{\mathrm{10}}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\right) \\ $$$$\mathrm{sin}\:\varphi=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}}\:\Rightarrow\varphi=\pi−\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}} \\ $$$$\mathrm{sin}\:\gamma=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}}\:\Rightarrow\gamma=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}} \\ $$$$\delta=\pi−\varphi−\gamma=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}} \\ $$$$\mathrm{cos}\:\delta=\frac{\sqrt{\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}\right)\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\delta=\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}\right)}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{sin}\:\delta=\frac{\sqrt{\mathrm{2}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)}−\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{sin}\:\delta=\frac{\mathrm{2}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}+\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${OB}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){r}+{AD}\:\mathrm{cos}\:\delta \\ $$$${BD}={AD}\:\mathrm{sin}\:\delta \\ $$$${OB}^{\mathrm{2}} +{BD}^{\mathrm{2}} ={OD}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){r}+{AD}\:\mathrm{cos}\:\delta\right]^{\mathrm{2}} +\left({AD}\:\mathrm{sin}\:\delta\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\left({AD}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\mathrm{cos}\:\delta\:{AD}+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\frac{{AD}}{{r}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\mathrm{cos}\:\delta\left(\frac{{AD}}{{r}}\right)+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{9}}{\:\sqrt{\mathrm{10}}−\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\frac{{AD}}{{r}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}\right)}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}\left(\frac{{AD}}{{r}}\right)+\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{9}}{\:\sqrt{\mathrm{10}}−\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\frac{{AD}}{{r}}\right)^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{14}+\mathrm{9}\sqrt{\mathrm{2}}\right)\left(\mathrm{1}+\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}\right)}{\mathrm{17}}\left(\frac{{AD}}{{r}}\right)−\mathrm{2}\left(\mathrm{4}+\sqrt{\mathrm{10}}−\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\frac{{AD}}{{r}}=−\frac{\left(\mathrm{14}+\mathrm{9}\sqrt{\mathrm{2}}\right)\left(\mathrm{1}+\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}\right)}{\mathrm{17}}+\sqrt{\frac{\left(\mathrm{14}+\mathrm{9}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }{\mathrm{17}^{\mathrm{2}} }+\mathrm{2}\left(\mathrm{4}+\sqrt{\mathrm{10}}−\sqrt{\mathrm{2}}\right)} \\ $$$$\frac{{AD}}{{r}}=\frac{\sqrt{\mathrm{2722}+\mathrm{578}\sqrt{\mathrm{10}}−\mathrm{312}\sqrt{\mathrm{2}}+\left(\mathrm{716}+\mathrm{504}\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}}−\left(\mathrm{14}+\mathrm{9}\sqrt{\mathrm{2}}\right)\left(\mathrm{1}+\sqrt{\mathrm{10}−\mathrm{7}\sqrt{\mathrm{2}}}\right)}{\mathrm{17}} \\ $$$${Area}\:{of}\:{triangle} \\ $$$${A}=\left({AD}\right)^{\mathrm{2}} \mathrm{sin}\:\delta\:\mathrm{cos}\:\delta \\ $$$$\approx\mathrm{1}.\mathrm{5956802}\:{r}^{\mathrm{2}} \\ $$$$\approx\mathrm{0}.\mathrm{0921051}{R}^{\mathrm{2}} \\ $$$$\approx\mathrm{5}.\mathrm{8947276} \\ $$
Commented by Tawa11 last updated on 20/Feb/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by ajfour last updated on 20/Feb/22
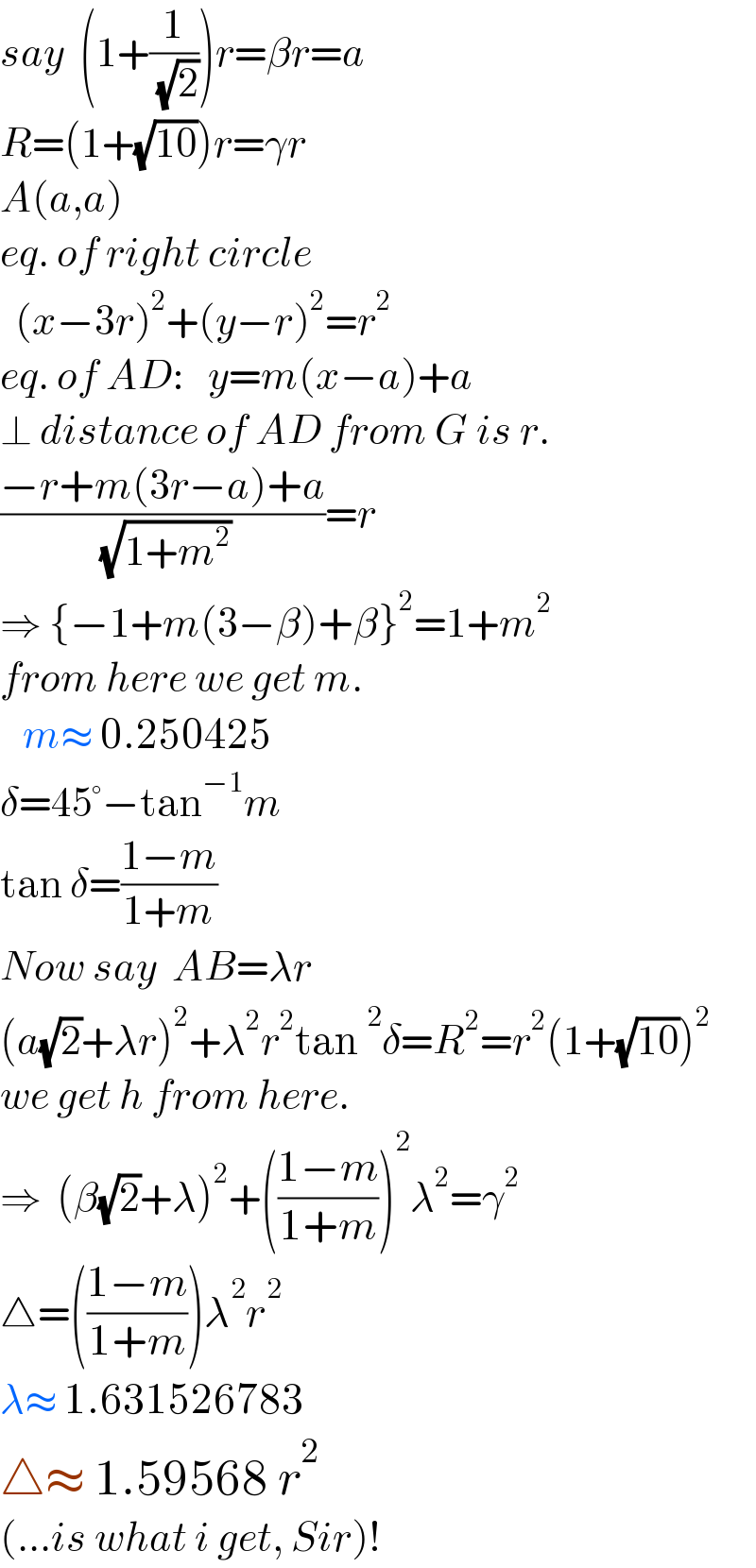
$${say}\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right){r}=\beta{r}={a} \\ $$$${R}=\left(\mathrm{1}+\sqrt{\mathrm{10}}\right){r}=\gamma{r} \\ $$$${A}\left({a},{a}\right) \\ $$$${eq}.\:{of}\:{right}\:{circle} \\ $$$$\:\:\left({x}−\mathrm{3}{r}\right)^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${eq}.\:{of}\:{AD}:\:\:\:{y}={m}\left({x}−{a}\right)+{a} \\ $$$$\bot\:{distance}\:{of}\:{AD}\:{from}\:{G}\:{is}\:{r}. \\ $$$$\frac{−{r}+{m}\left(\mathrm{3}{r}−{a}\right)+{a}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}={r} \\ $$$$\Rightarrow\:\left\{−\mathrm{1}+{m}\left(\mathrm{3}−\beta\right)+\beta\right\}^{\mathrm{2}} =\mathrm{1}+{m}^{\mathrm{2}} \\ $$$${from}\:{here}\:{we}\:{get}\:{m}. \\ $$$$\:\:\:{m}\approx\:\mathrm{0}.\mathrm{250425} \\ $$$$\delta=\mathrm{45}°−\mathrm{tan}^{−\mathrm{1}} {m} \\ $$$$\mathrm{tan}\:\delta=\frac{\mathrm{1}−{m}}{\mathrm{1}+{m}} \\ $$$${Now}\:{say}\:\:{AB}=\lambda{r} \\ $$$$\left({a}\sqrt{\mathrm{2}}+\lambda{r}\right)^{\mathrm{2}} +\lambda^{\mathrm{2}} {r}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \delta={R}^{\mathrm{2}} ={r}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{10}}\right)^{\mathrm{2}} \\ $$$${we}\:{get}\:{h}\:{from}\:{here}. \\ $$$$\Rightarrow\:\:\left(\beta\sqrt{\mathrm{2}}+\lambda\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}−{m}}{\mathrm{1}+{m}}\right)^{\mathrm{2}} \lambda^{\mathrm{2}} =\gamma^{\mathrm{2}} \\ $$$$\bigtriangleup=\left(\frac{\mathrm{1}−{m}}{\mathrm{1}+{m}}\right)\lambda^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$$\lambda\approx\:\mathrm{1}.\mathrm{631526783} \\ $$$$\bigtriangleup\approx\:\mathrm{1}.\mathrm{59568}\:{r}^{\mathrm{2}} \\ $$$$\left(…{is}\:{what}\:{i}\:{get},\:{Sir}\right)! \\ $$
Commented by mr W last updated on 20/Feb/22

$${fine}\:{sir}! \\ $$$${can}\:{A}\approx\mathrm{1}.\mathrm{5956802}\:{r}^{\mathrm{2}} \:{be}\:{comfirmed}? \\ $$
Commented by ajfour last updated on 20/Feb/22
$${yeah},\:{its}\:{absolutely}\:{confirmed}! \\ $$
Commented by ajfour last updated on 20/Feb/22
Awesome solution sir.
