Menu Close

Question-166419

Tinku Tara 0 Comments
Pin




Question Number 166419 by ajfour last updated on 19/Feb/22
Commented by ajfour last updated on 19/Feb/22
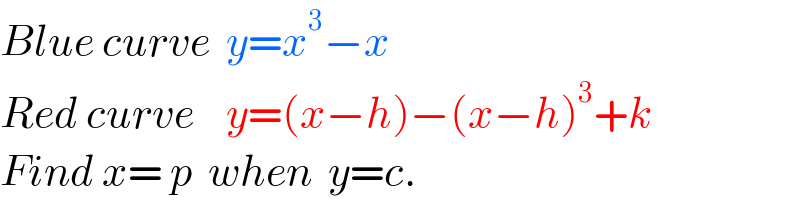
Blue curve y=x^3 −x Red curve y=(x−h)−(x−h)^3 +k Find x= p when y=c.
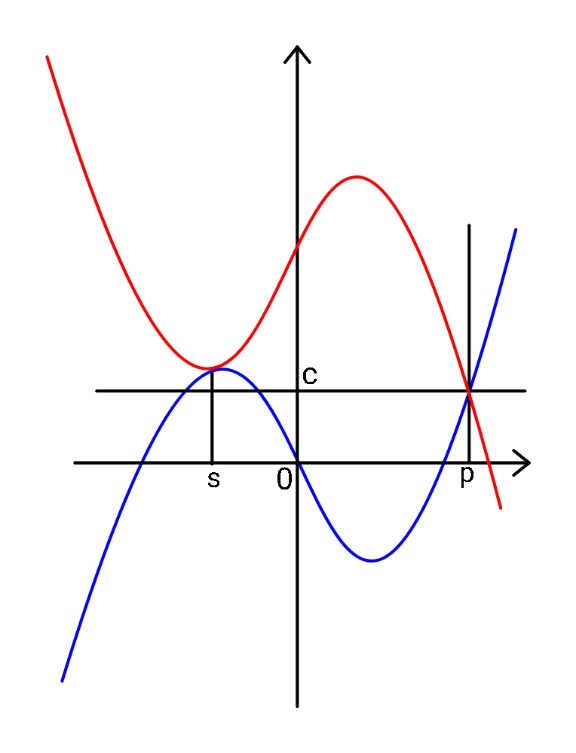
$${Blue}\:{curve}\:\:{y}={x}^{\mathrm{3}} −{x} \\ $$$${Red}\:{curve}\:\:\:\:{y}=\left({x}−{h}\right)−\left({x}−{h}\right)^{\mathrm{3}} +{k} \\ $$$${Find}\:{x}=\:{p}\:\:{when}\:\:{y}={c}. \\ $$
Answered by ajfour last updated on 20/Feb/22
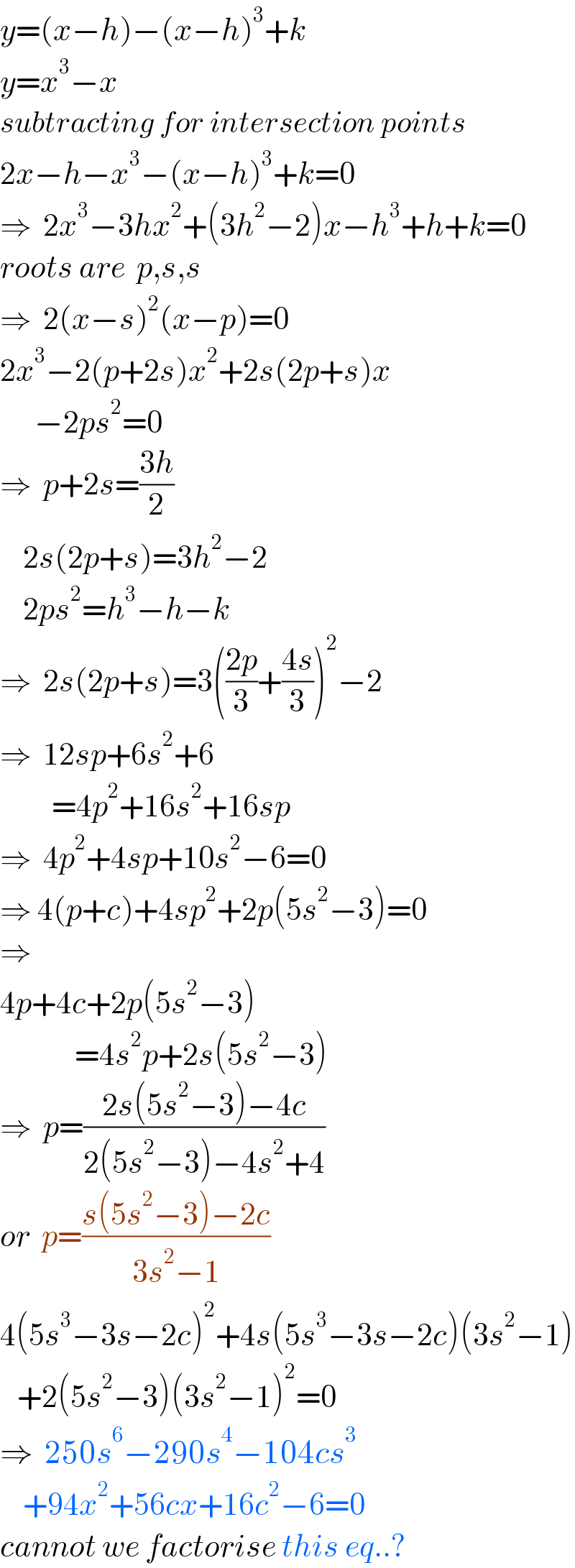
y=(x−h)−(x−h)^3 +k y=x^3 −x subtracting for intersection points 2x−h−x^3 −(x−h)^3 +k=0 ⇒ 2x^3 −3hx^2 +(3h^2 −2)x−h^3 +h+k=0 roots are p,s,s ⇒ 2(x−s)^2 (x−p)=0 2x^3 −2(p+2s)x^2 +2s(2p+s)x −2ps^2 =0 ⇒ p+2s=((3h)/2) 2s(2p+s)=3h^2 −2 2ps^2 =h^3 −h−k ⇒ 2s(2p+s)=3(((2p)/3)+((4s)/3))^2 −2 ⇒ 12sp+6s^2 +6 =4p^2 +16s^2 +16sp ⇒ 4p^2 +4sp+10s^2 −6=0 ⇒ 4(p+c)+4sp^2 +2p(5s^2 −3)=0 ⇒ 4p+4c+2p(5s^2 −3) =4s^2 p+2s(5s^2 −3) ⇒ p=((2s(5s^2 −3)−4c)/(2(5s^2 −3)−4s^2 +4)) or p=((s(5s^2 −3)−2c)/(3s^2 −1)) 4(5s^3 −3s−2c)^2 +4s(5s^3 −3s−2c)(3s^2 −1) +2(5s^2 −3)(3s^2 −1)^2 =0 ⇒ 250s^6 −290s^4 −104cs^3 +94x^2 +56cx+16c^2 −6=0 cannot we factorise this eq..?
$${y}=\left({x}−{h}\right)−\left({x}−{h}\right)^{\mathrm{3}} +{k} \\ $$$${y}={x}^{\mathrm{3}} −{x} \\ $$$${subtracting}\:{for}\:{intersection}\:{points} \\ $$$$\mathrm{2}{x}−{h}−{x}^{\mathrm{3}} −\left({x}−{h}\right)^{\mathrm{3}} +{k}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{x}^{\mathrm{3}} −\mathrm{3}{hx}^{\mathrm{2}} +\left(\mathrm{3}{h}^{\mathrm{2}} −\mathrm{2}\right){x}−{h}^{\mathrm{3}} +{h}+{k}=\mathrm{0} \\ $$$${roots}\:{are}\:\:{p},{s},{s} \\ $$$$\Rightarrow\:\:\mathrm{2}\left({x}−{s}\right)^{\mathrm{2}} \left({x}−{p}\right)=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}\left({p}+\mathrm{2}{s}\right){x}^{\mathrm{2}} +\mathrm{2}{s}\left(\mathrm{2}{p}+{s}\right){x} \\ $$$$\:\:\:\:\:\:−\mathrm{2}{ps}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:{p}+\mathrm{2}{s}=\frac{\mathrm{3}{h}}{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{2}{s}\left(\mathrm{2}{p}+{s}\right)=\mathrm{3}{h}^{\mathrm{2}} −\mathrm{2} \\ $$$$\:\:\:\:\mathrm{2}{ps}^{\mathrm{2}} ={h}^{\mathrm{3}} −{h}−{k} \\ $$$$\Rightarrow\:\:\mathrm{2}{s}\left(\mathrm{2}{p}+{s}\right)=\mathrm{3}\left(\frac{\mathrm{2}{p}}{\mathrm{3}}+\frac{\mathrm{4}{s}}{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow\:\:\mathrm{12}{sp}+\mathrm{6}{s}^{\mathrm{2}} +\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}{p}^{\mathrm{2}} +\mathrm{16}{s}^{\mathrm{2}} +\mathrm{16}{sp} \\ $$$$\Rightarrow\:\:\mathrm{4}{p}^{\mathrm{2}} +\mathrm{4}{sp}+\mathrm{10}{s}^{\mathrm{2}} −\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{4}\left({p}+{c}\right)+\mathrm{4}{sp}^{\mathrm{2}} +\mathrm{2}{p}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{p}+\mathrm{4}{c}+\mathrm{2}{p}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{s}^{\mathrm{2}} {p}+\mathrm{2}{s}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\Rightarrow\:\:{p}=\frac{\mathrm{2}{s}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{4}{c}}{\mathrm{2}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{4}{s}^{\mathrm{2}} +\mathrm{4}} \\ $$$${or}\:\:{p}=\frac{{s}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right)−\mathrm{2}{c}}{\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{4}\left(\mathrm{5}{s}^{\mathrm{3}} −\mathrm{3}{s}−\mathrm{2}{c}\right)^{\mathrm{2}} +\mathrm{4}{s}\left(\mathrm{5}{s}^{\mathrm{3}} −\mathrm{3}{s}−\mathrm{2}{c}\right)\left(\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:+\mathrm{2}\left(\mathrm{5}{s}^{\mathrm{2}} −\mathrm{3}\right)\left(\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{250}{s}^{\mathrm{6}} −\mathrm{290}{s}^{\mathrm{4}} −\mathrm{104}{cs}^{\mathrm{3}} \\ $$$$\:\:\:\:+\mathrm{94}{x}^{\mathrm{2}} +\mathrm{56}{cx}+\mathrm{16}{c}^{\mathrm{2}} −\mathrm{6}=\mathrm{0} \\ $$$${cannot}\:{we}\:{factorise}\:{this}\:{eq}..? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *