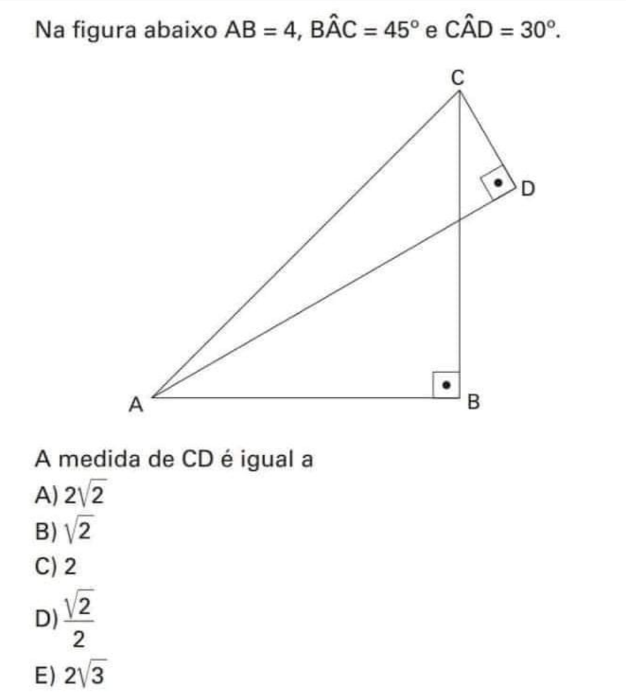
Question Number 166424 by leicianocosta last updated on 20/Feb/22
Commented by cortano1 last updated on 20/Feb/22
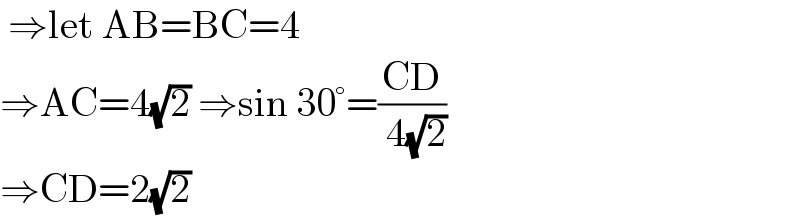
$$\:\Rightarrow\mathrm{let}\:\mathrm{AB}=\mathrm{BC}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{AC}=\mathrm{4}\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:\mathrm{30}°=\frac{\mathrm{CD}}{\:\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{CD}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$
Commented by som(math1967) last updated on 20/Feb/22

$${AB}=\mathrm{4}\: \\ $$
Commented by cortano1 last updated on 20/Feb/22

$$\mathrm{owh}\:\mathrm{yes} \\ $$
Answered by som(math1967) last updated on 20/Feb/22
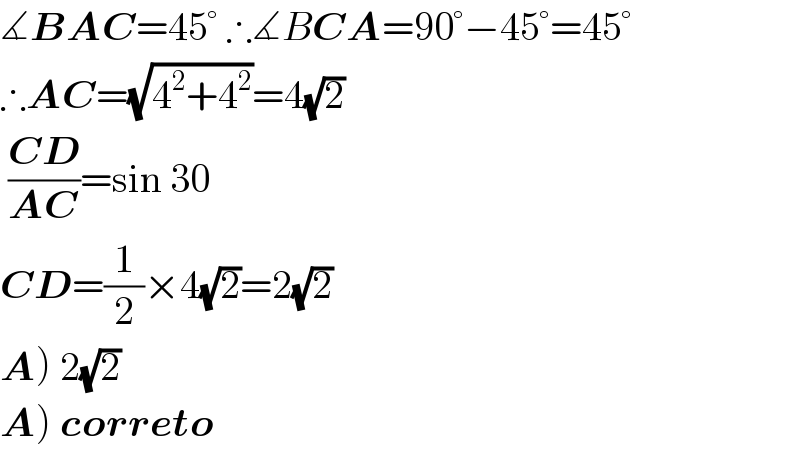
$$\measuredangle\boldsymbol{{BAC}}=\mathrm{45}°\:\therefore\measuredangle{B}\boldsymbol{{CA}}=\mathrm{90}°−\mathrm{45}°=\mathrm{45}° \\ $$$$\therefore\boldsymbol{{AC}}=\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }=\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$\:\frac{\boldsymbol{{CD}}}{\boldsymbol{{AC}}}=\mathrm{sin}\:\mathrm{30} \\ $$$$\boldsymbol{{CD}}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}\sqrt{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\left.\boldsymbol{{A}}\right)\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\left.\boldsymbol{{A}}\right)\:\boldsymbol{{correto}} \\ $$
