Question Number 166520 by ajfour last updated on 21/Feb/22

Commented by ajfour last updated on 21/Feb/22

$${If}\:{the}\:{circles}\:{have}\:{radii}\:{a},{b},{c} \\ $$$$\:{find}\:{maximum}\:{side}\:{length}\:{of} \\ $$$${such}\:{an}\:{equilateral}\:{triangle}. \\ $$
Commented by mr W last updated on 22/Feb/22

$${the}\:{general}\:{case}\:{see}\:{Q}\mathrm{16194}. \\ $$
Answered by mr W last updated on 21/Feb/22

Commented by mr W last updated on 21/Feb/22

$${this}\:{is}\:{to}\:{find}\:{the}\:{triangle}\:{with}\:{the} \\ $$$${maximum}\:{area},\:{not}\:{the}\:{maximum} \\ $$$${equilateral}\:{triangle}. \\ $$$$ \\ $$$$\mathrm{tan}\:\alpha=\frac{\left(\mathrm{1}+\mathrm{cos}\:\beta\right){b}+\left(\mathrm{1}+\mathrm{cos}\:\gamma\right){c}}{\left(\mathrm{1}+\mathrm{sin}\:\beta\right){b}+\left(\mathrm{1}+\mathrm{sin}\:\gamma\right){c}} \\ $$$$\mathrm{cos}\:\left(\alpha+\gamma\right)=\left(\frac{{b}}{{c}}+\mathrm{1}\right)\left(\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha\right)−\frac{{b}}{{c}}\:\mathrm{cos}\:\left(\alpha+\beta\right) \\ $$$$ \\ $$$$\mathrm{tan}\:\beta=\frac{\left(\mathrm{1}+\mathrm{cos}\:\alpha\right){a}+\left(\mathrm{1}+\mathrm{cos}\:\gamma\right){c}}{\left(\mathrm{1}+\mathrm{sin}\:\alpha\right){a}−\left(\mathrm{1}+\mathrm{sin}\:\gamma\right){c}} \\ $$$$\mathrm{cos}\:\left(\beta−\gamma\right)=\left(\frac{{a}}{{c}}−\mathrm{1}\right)\mathrm{sin}\:\beta−\left(\frac{{a}}{{c}}+\mathrm{1}\right)\mathrm{cos}\:\beta−\frac{{a}}{{c}}\:\mathrm{cos}\:\left(\alpha+\beta\right) \\ $$$$ \\ $$$$\mathrm{tan}\:\gamma=\frac{\left(\mathrm{1}+\mathrm{cos}\:\alpha\right){a}−\left(\mathrm{1}+\mathrm{cos}\:\beta\right){b}}{\left(\mathrm{1}+\mathrm{sin}\:\alpha\right){a}+\left(\mathrm{1}+\mathrm{sin}\:\beta\right){b}} \\ $$$$ \\ $$$${solve}\:{for}\:\alpha,\beta,\gamma. \\ $$
Commented by mr W last updated on 21/Feb/22
Commented by mr W last updated on 21/Feb/22

Answered by mr W last updated on 22/Feb/22

Commented by mr W last updated on 22/Feb/22
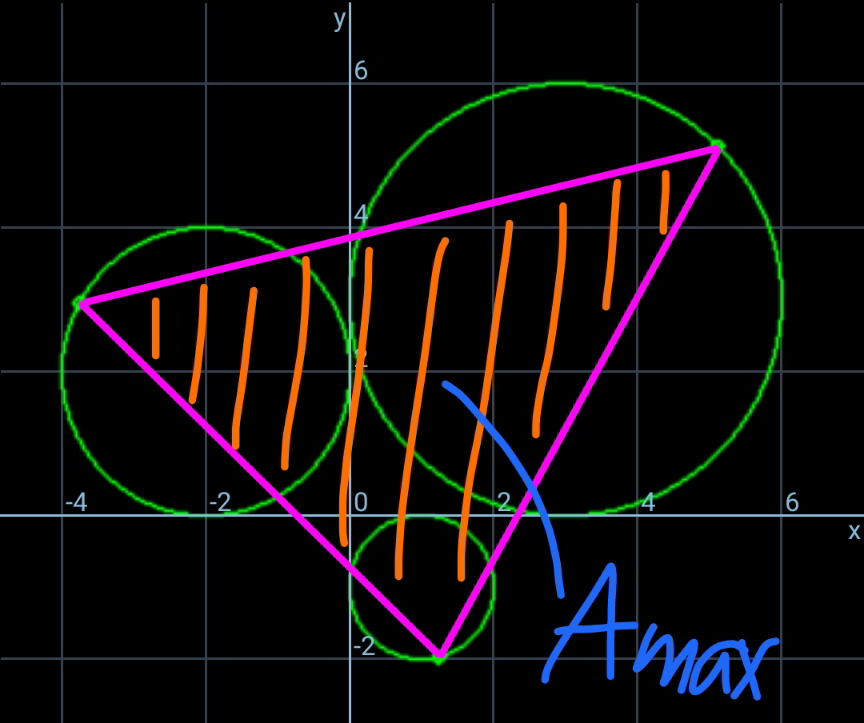
^2 =a^2 (a−h)^2 x−a=±((a(a−h))/( (√((a−h)^2 +(a−k)^2 )))) x_P =a+(a/( (√(1+(((a−k)/(a−h)))^2 )))) y_P =a+(a/( (√(1+(((a−h)/(a−k)))^2 )))) eqn. of GB: ((y−k)/(b−k))=((x−h)/(−b−h)) −(b+h)y=(b−k)x−b(h+k) eqn. of circle B: (x+b)^2 +(y−b)^2 =b^2 [(b+h)^2 +(b−k)^2 ](x+b)^2 =b^2 (b+h)^2 x+b=±((b(b+h))/( (√((b+h)^2 +(b−k)^2 )))) x_Q =−b−(b/( (√(1+(((b−k)/(b+h)))^2 )))) y_Q =b+(b/( (√(1+(((b+h)/(b−k)))^2 )))) eqn. of GC: ((y−k)/(−c−k))=((x−h)/(c−h)) (c−h)y=−(c+k)x+c(h+k) eqn. of circle C: (x−c)^2 +(y+c)^2 =c^2 [(c−h)^2 +(c+k)^2 ](x−c)^2 =c^2 (c−h)^2 x−c=±((c(c−h))/( (√((c−h)^2 +(c+k)^2 )))) x_R =c+(c/( (√(1+(((c+k)/(c−h)))^2 )))) y_R =−c−(c/( (√(1+(((c−h)/(c+k)))^2 )))) s^2 =(x_P −x_Q )^2 +(y_P −y_Q )^2 s^2 =(a+b+(a/( (√(1+(((a−k)/(a−h)))^2 ))))+(b/( (√(1+(((b−k)/(b+h)))^2 )))))^2 +(a−b+(a/( (√(1+(((a−h)/(a−k)))^2 ))))−(b/( (√(1+(((b+h)/(b−k)))^2 )))))^2 s^2 =(x_P −x_R )^2 +(y_P −y_R )^2 s^2 =(a−c+(a/( (√(1+(((a−k)/(a−h)))^2 ))))−(c/( (√(1+(((c+k)/(c−h)))^2 )))))^2 +(a+c+(a/( (√(1+(((a−h)/(a−k)))^2 ))))+(c/( (√(1+(((c−h)/(c+k)))^2 )))))^2 s^2 =(x_Q −x_R )^2 +(y_Q −y_R )^2 s^2 =(b+c+(b/( (√(1+(((b−k)/(b+h)))^2 ))))+(c/( (√(1+(((c+k)/(c−h)))^2 )))))^2 +(b+c+(b/( (√(1+(((b+h)/(b−k)))^2 ))))+(c/( (√(1+(((c−h)/(c+k)))^2 )))))^2 solve for h,k,s ....](https://www.tinkutara.com/question/Q166544.png)
$${A}\left({a},{a}\right) \\ $$$${B}\left(−{b},{b}\right) \\ $$$${C}\left({c},−{c}\right) \\ $$$${say}\:{G}\left({h},{k}\right) \\ $$$${eqn}.\:{of}\:{GP}: \\ $$$$\frac{{y}−{k}}{{a}−{k}}=\frac{{x}−{h}}{{a}−{h}} \\ $$$$\left({a}−{h}\right){y}=\left({a}−{k}\right){x}+{a}\left({k}−{h}\right) \\ $$$${y}=\frac{{a}−{k}}{{a}−{h}}{x}+\frac{{a}\left({k}−{h}\right)}{{a}−{h}} \\ $$$${eqn}.\:{of}\:{circle}\:{A}: \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +\left(\frac{{a}−{k}}{{a}−{h}}{x}+\frac{{a}\left({k}−{h}\right)}{{a}−{h}}−{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\left[\left({a}−{h}\right)^{\mathrm{2}} +\left({a}−{k}\right)^{\mathrm{2}} \right]\left({x}−{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \left({a}−{h}\right)^{\mathrm{2}} \\ $$$${x}−{a}=\pm\frac{{a}\left({a}−{h}\right)}{\:\sqrt{\left({a}−{h}\right)^{\mathrm{2}} +\left({a}−{k}\right)^{\mathrm{2}} }} \\ $$$${x}_{{P}} ={a}+\frac{{a}}{\:\sqrt{\mathrm{1}+\left(\frac{{a}−{k}}{{a}−{h}}\right)^{\mathrm{2}} }} \\ $$$${y}_{{P}} ={a}+\frac{{a}}{\:\sqrt{\mathrm{1}+\left(\frac{{a}−{h}}{{a}−{k}}\right)^{\mathrm{2}} }} \\ $$$${eqn}.\:{of}\:{GB}: \\ $$$$\frac{{y}−{k}}{{b}−{k}}=\frac{{x}−{h}}{−{b}−{h}} \\ $$$$−\left({b}+{h}\right){y}=\left({b}−{k}\right){x}−{b}\left({h}+{k}\right) \\ $$$${eqn}.\:{of}\:{circle}\:{B}: \\ $$$$\left({x}+{b}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\left[\left({b}+{h}\right)^{\mathrm{2}} +\left({b}−{k}\right)^{\mathrm{2}} \right]\left({x}+{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \left({b}+{h}\right)^{\mathrm{2}} \\ $$$${x}+{b}=\pm\frac{{b}\left({b}+{h}\right)}{\:\sqrt{\left({b}+{h}\right)^{\mathrm{2}} +\left({b}−{k}\right)^{\mathrm{2}} }} \\ $$$${x}_{{Q}} =−{b}−\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\frac{{b}−{k}}{{b}+{h}}\right)^{\mathrm{2}} }} \\ $$$${y}_{{Q}} ={b}+\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\frac{{b}+{h}}{{b}−{k}}\right)^{\mathrm{2}} }} \\ $$$${eqn}.\:{of}\:{GC}: \\ $$$$\frac{{y}−{k}}{−{c}−{k}}=\frac{{x}−{h}}{{c}−{h}} \\ $$$$\left({c}−{h}\right){y}=−\left({c}+{k}\right){x}+{c}\left({h}+{k}\right) \\ $$$${eqn}.\:{of}\:{circle}\:{C}: \\ $$$$\left({x}−{c}\right)^{\mathrm{2}} +\left({y}+{c}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\left[\left({c}−{h}\right)^{\mathrm{2}} +\left({c}+{k}\right)^{\mathrm{2}} \right]\left({x}−{c}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \left({c}−{h}\right)^{\mathrm{2}} \\ $$$${x}−{c}=\pm\frac{{c}\left({c}−{h}\right)}{\:\sqrt{\left({c}−{h}\right)^{\mathrm{2}} +\left({c}+{k}\right)^{\mathrm{2}} }} \\ $$$${x}_{{R}} ={c}+\frac{{c}}{\:\sqrt{\mathrm{1}+\left(\frac{{c}+{k}}{{c}−{h}}\right)^{\mathrm{2}} }} \\ $$$${y}_{{R}} =−{c}−\frac{{c}}{\:\sqrt{\mathrm{1}+\left(\frac{{c}−{h}}{{c}+{k}}\right)^{\mathrm{2}} }} \\ $$$$ \\ $$$${s}^{\mathrm{2}} =\left({x}_{{P}} −{x}_{{Q}} \right)^{\mathrm{2}} +\left({y}_{{P}} −{y}_{{Q}} \right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({a}+{b}+\frac{{a}}{\:\sqrt{\mathrm{1}+\left(\frac{{a}−{k}}{{a}−{h}}\right)^{\mathrm{2}} }}+\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\frac{{b}−{k}}{{b}+{h}}\right)^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left({a}−{b}+\frac{{a}}{\:\sqrt{\mathrm{1}+\left(\frac{{a}−{h}}{{a}−{k}}\right)^{\mathrm{2}} }}−\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\frac{{b}+{h}}{{b}−{k}}\right)^{\mathrm{2}} }}\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({x}_{{P}} −{x}_{{R}} \right)^{\mathrm{2}} +\left({y}_{{P}} −{y}_{{R}} \right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({a}−{c}+\frac{{a}}{\:\sqrt{\mathrm{1}+\left(\frac{{a}−{k}}{{a}−{h}}\right)^{\mathrm{2}} }}−\frac{{c}}{\:\sqrt{\mathrm{1}+\left(\frac{{c}+{k}}{{c}−{h}}\right)^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left({a}+{c}+\frac{{a}}{\:\sqrt{\mathrm{1}+\left(\frac{{a}−{h}}{{a}−{k}}\right)^{\mathrm{2}} }}+\frac{{c}}{\:\sqrt{\mathrm{1}+\left(\frac{{c}−{h}}{{c}+{k}}\right)^{\mathrm{2}} }}\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({x}_{{Q}} −{x}_{{R}} \right)^{\mathrm{2}} +\left({y}_{{Q}} −{y}_{{R}} \right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({b}+{c}+\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\frac{{b}−{k}}{{b}+{h}}\right)^{\mathrm{2}} }}+\frac{{c}}{\:\sqrt{\mathrm{1}+\left(\frac{{c}+{k}}{{c}−{h}}\right)^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left({b}+{c}+\frac{{b}}{\:\sqrt{\mathrm{1}+\left(\frac{{b}+{h}}{{b}−{k}}\right)^{\mathrm{2}} }}+\frac{{c}}{\:\sqrt{\mathrm{1}+\left(\frac{{c}−{h}}{{c}+{k}}\right)^{\mathrm{2}} }}\right)^{\mathrm{2}} \\ $$$${solve}\:{for}\:{h},{k},{s} \\ $$$$…. \\ $$
Commented by ajfour last updated on 22/Feb/22
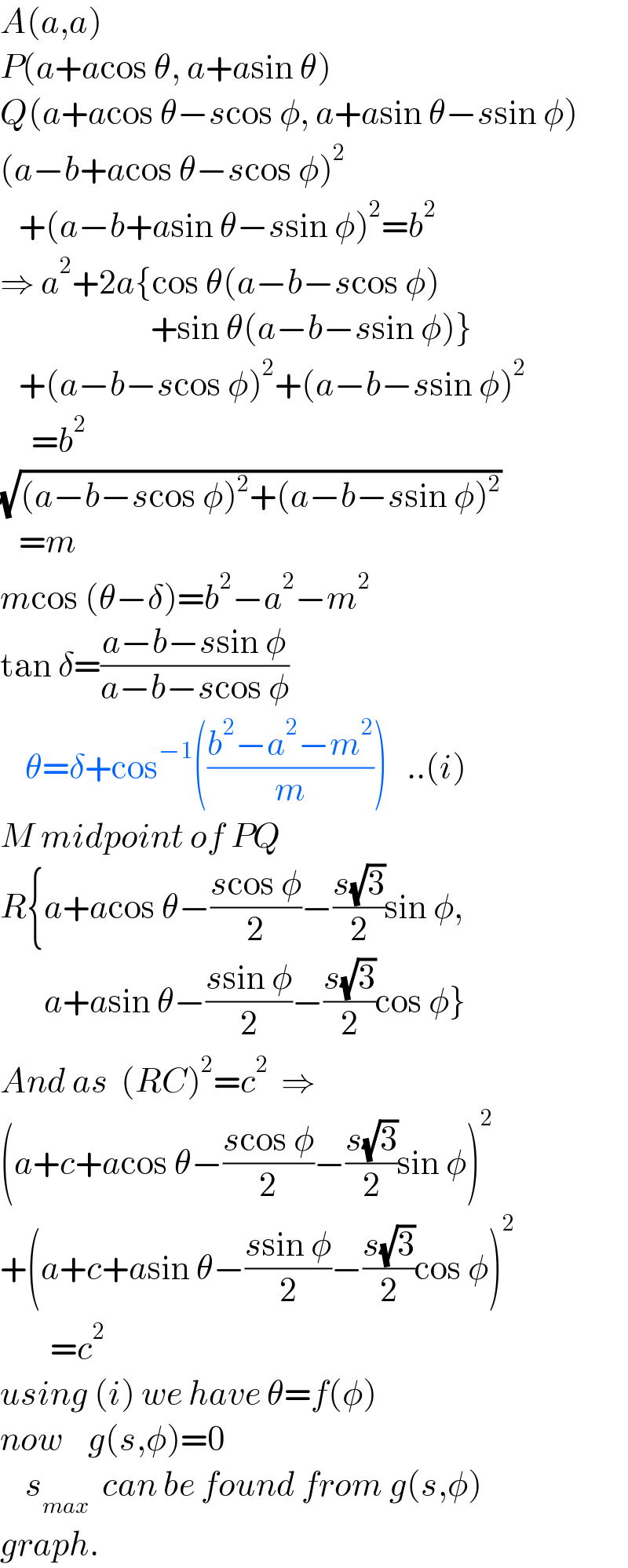
$${A}\left({a},{a}\right) \\ $$$${P}\left({a}+{a}\mathrm{cos}\:\theta,\:{a}+{a}\mathrm{sin}\:\theta\right) \\ $$$${Q}\left({a}+{a}\mathrm{cos}\:\theta−{s}\mathrm{cos}\:\phi,\:{a}+{a}\mathrm{sin}\:\theta−{s}\mathrm{sin}\:\phi\right) \\ $$$$\left({a}−{b}+{a}\mathrm{cos}\:\theta−{s}\mathrm{cos}\:\phi\right)^{\mathrm{2}} \\ $$$$\:\:\:+\left({a}−{b}+{a}\mathrm{sin}\:\theta−{s}\mathrm{sin}\:\phi\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} +\mathrm{2}{a}\left\{\mathrm{cos}\:\theta\left({a}−{b}−{s}\mathrm{cos}\:\phi\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:\theta\left({a}−{b}−{s}\mathrm{sin}\:\phi\right)\right\} \\ $$$$\:\:\:+\left({a}−{b}−{s}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({a}−{b}−{s}\mathrm{sin}\:\phi\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:={b}^{\mathrm{2}} \\ $$$$\sqrt{\left({a}−{b}−{s}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({a}−{b}−{s}\mathrm{sin}\:\phi\right)^{\mathrm{2}} } \\ $$$$\:\:\:={m} \\ $$$${m}\mathrm{cos}\:\left(\theta−\delta\right)={b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{m}^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\delta=\frac{{a}−{b}−{s}\mathrm{sin}\:\phi}{{a}−{b}−{s}\mathrm{cos}\:\phi} \\ $$$$\:\:\:\:\theta=\delta+\mathrm{cos}^{−\mathrm{1}} \left(\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{m}^{\mathrm{2}} }{{m}}\right)\:\:\:..\left({i}\right) \\ $$$${M}\:{midpoint}\:{of}\:{PQ} \\ $$$${R}\left\{{a}+{a}\mathrm{cos}\:\theta−\frac{{s}\mathrm{cos}\:\phi}{\mathrm{2}}−\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\phi,\right. \\ $$$$\left.\:\:\:\:\:\:\:{a}+{a}\mathrm{sin}\:\theta−\frac{{s}\mathrm{sin}\:\phi}{\mathrm{2}}−\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\phi\right\} \\ $$$${And}\:{as}\:\:\left({RC}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \:\:\Rightarrow \\ $$$$\left({a}+{c}+{a}\mathrm{cos}\:\theta−\frac{{s}\mathrm{cos}\:\phi}{\mathrm{2}}−\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\phi\right)^{\mathrm{2}} \\ $$$$+\left({a}+{c}+{a}\mathrm{sin}\:\theta−\frac{{s}\mathrm{sin}\:\phi}{\mathrm{2}}−\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\phi\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:={c}^{\mathrm{2}} \\ $$$${using}\:\left({i}\right)\:{we}\:{have}\:\theta={f}\left(\phi\right) \\ $$$${now}\:\:\:\:{g}\left({s},\phi\right)=\mathrm{0} \\ $$$$\:\:\:\:{s}_{{max}} \:\:{can}\:{be}\:{found}\:{from}\:{g}\left({s},\phi\right) \\ $$$${graph}. \\ $$
Commented by Tawa11 last updated on 22/Feb/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
