Question Number 166570 by cortano1 last updated on 22/Feb/22
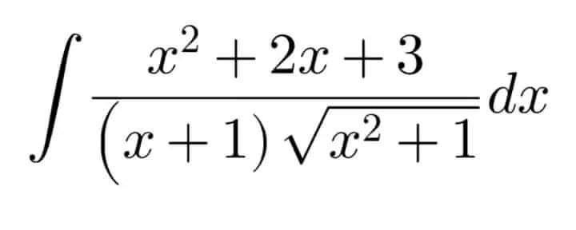
Answered by bobhans last updated on 22/Feb/22
![I=∫ (((x+1)^2 +2)/((x+1)(√(x^2 +1)))) dx = ∫((x+1)/( (√(x^2 +1))))dx+∫(2/((x+1)(√(x^2 +1))))dx I_1 =(1/2)∫ ((d(x^2 +1))/( (√(x^2 +1))))=(√(x^2 +1))+c_1 I_2 =∫ (dx/( (√(x^2 +1)))) , [ x=tan θ ] I_2 =∫ ((sec^2 θ)/(sec θ)) dθ = ln ∣x+(√(x^2 +1)) ∣+c_2 I_3 =∫ (2/((x+1)(√(x^2 +1))))dx , [ x=tan y ] I_3 =2∫ ((sec^2 y)/((1+tan y)sec y)) dy=2∫ ((sec y)/(1+tan y)) dy I_3 =2∫(dy/(cos y+sin y))=2∫(dy/( (√2) cos (y−45°))) I_3 =(√2) ∫ sec (y−45°)dy=(√2) ln ∣((1+sin (y−45°))/(cos (y−45°)))∣+c_3 I_3 =(√2) ln ∣(((√2)(1+(1/( (√2)))sin y−(1/( (√2)))cos y))/(cos y+sin y))∣+c_3 I_3 =(√2) ln ∣(((√2)+sin y−cos y)/(cos y+sin y))∣+c_3](https://www.tinkutara.com/question/Q166571.png)
$$\:\mathrm{I}=\int\:\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:\mathrm{dx}\:=\:\int\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dx}+\int\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{c}_{\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{2}} =\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:,\:\left[\:\mathrm{x}=\mathrm{tan}\:\theta\:\right] \\ $$$$\mathrm{I}_{\mathrm{2}} =\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta}{\mathrm{sec}\:\theta}\:\mathrm{d}\theta\:=\:\mathrm{ln}\:\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\mid+\mathrm{c}_{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\int\:\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\mathrm{dx}\:,\:\left[\:\mathrm{x}=\mathrm{tan}\:\mathrm{y}\:\right] \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{2}\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{y}}{\left(\mathrm{1}+\mathrm{tan}\:\mathrm{y}\right)\mathrm{sec}\:\mathrm{y}}\:\mathrm{dy}=\mathrm{2}\int\:\frac{\mathrm{sec}\:\mathrm{y}}{\mathrm{1}+\mathrm{tan}\:\mathrm{y}}\:\mathrm{dy} \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{2}\int\frac{\mathrm{dy}}{\mathrm{cos}\:\mathrm{y}+\mathrm{sin}\:\mathrm{y}}=\mathrm{2}\int\frac{\mathrm{dy}}{\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left(\mathrm{y}−\mathrm{45}°\right)} \\ $$$$\mathrm{I}_{\mathrm{3}} =\sqrt{\mathrm{2}}\:\int\:\mathrm{sec}\:\left(\mathrm{y}−\mathrm{45}°\right)\mathrm{dy}=\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{sin}\:\left(\mathrm{y}−\mathrm{45}°\right)}{\mathrm{cos}\:\left(\mathrm{y}−\mathrm{45}°\right)}\mid+\mathrm{c}_{\mathrm{3}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sin}\:\mathrm{y}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{cos}\:\mathrm{y}\right)}{\mathrm{cos}\:\mathrm{y}+\mathrm{sin}\:\mathrm{y}}\mid+\mathrm{c}_{\mathrm{3}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\sqrt{\mathrm{2}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}}+\mathrm{sin}\:\mathrm{y}−\mathrm{cos}\:\mathrm{y}}{\mathrm{cos}\:\mathrm{y}+\mathrm{sin}\:\mathrm{y}}\mid+\mathrm{c}_{\mathrm{3}} \\ $$
Commented by peter frank last updated on 22/Feb/22

$$\mathrm{great} \\ $$
Commented by MJS_new last updated on 23/Feb/22
![I_3 =2∫(dx/((x+1)(√(x^2 +1))))= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/t)dt] =4∫(dt/(t^2 +2t−1))=(√2)∫((1/(t+1−(√2)))−(1/(t+1+(√2))))dt= =(√2)ln ((t+1−(√2))/(t+1+(√2))) = =(√2)ln ∣((x−1+(√(2(x^2 +1))))/(x+1))∣ +C but of course you get the same: (((√2)+sin y −cos y)/(cos y +sin y))= [y=arctan x] =((x−1+(√(2(x^2 +1))))/(x+1))](https://www.tinkutara.com/question/Q166607.png)
$${I}_{\mathrm{3}} =\mathrm{2}\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{t}}{dt}\right] \\ $$$$=\mathrm{4}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}=\sqrt{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{t}+\mathrm{1}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{t}+\mathrm{1}+\sqrt{\mathrm{2}}}\right){dt}= \\ $$$$=\sqrt{\mathrm{2}}\mathrm{ln}\:\frac{{t}+\mathrm{1}−\sqrt{\mathrm{2}}}{{t}+\mathrm{1}+\sqrt{\mathrm{2}}}\:= \\ $$$$=\sqrt{\mathrm{2}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}+\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}{{x}+\mathrm{1}}\mid\:+{C} \\ $$$$\mathrm{but}\:\mathrm{of}\:\mathrm{course}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}: \\ $$$$\frac{\sqrt{\mathrm{2}}+\mathrm{sin}\:{y}\:−\mathrm{cos}\:{y}}{\mathrm{cos}\:{y}\:+\mathrm{sin}\:{y}}= \\ $$$$\:\:\:\:\:\left[{y}=\mathrm{arctan}\:{x}\right] \\ $$$$=\frac{{x}−\mathrm{1}+\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}{{x}+\mathrm{1}} \\ $$
