Question Number 166583 by ajfour last updated on 22/Feb/22
Answered by ajfour last updated on 23/Feb/22
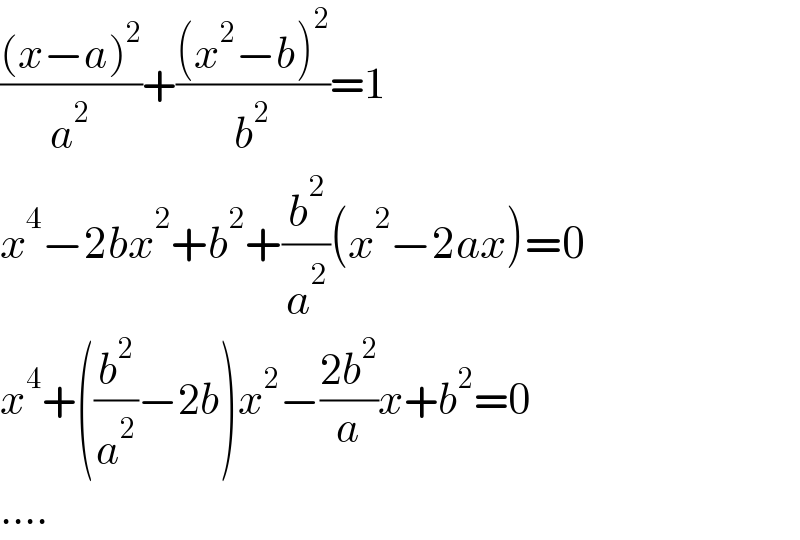
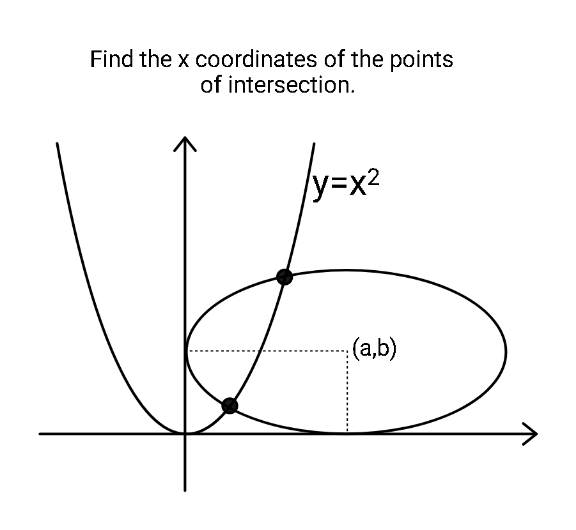
$$\frac{\left({x}−{a}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({x}^{\mathrm{2}} −{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${x}^{\mathrm{4}} −\mathrm{2}{bx}^{\mathrm{2}} +{b}^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left({x}^{\mathrm{2}} −\mathrm{2}{ax}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{2}{b}\right){x}^{\mathrm{2}} −\frac{\mathrm{2}{b}^{\mathrm{2}} }{{a}}{x}+{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$…. \\ $$
Commented by MJS_new last updated on 27/Feb/22

$$\mathrm{yes}.\:\mathrm{we}\:\mathrm{can}\:\mathrm{test}\:\mathrm{this}\:\left(\mathrm{remember},\:\mathrm{I}\:\mathrm{posted}\right. \\ $$$$\mathrm{the}\:\mathrm{conditions}\:\mathrm{for}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{combinations} \\ $$$$\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:{x}^{\mathrm{4}} +{px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0}\:\mathrm{some}\:\mathrm{time} \\ $$$$\left.\mathrm{ago}\right)\:\mathrm{and}\:\mathrm{find}\:\mathrm{that}\:\mathrm{for}\:{a},\:{b}\:\mathrm{it}\:\mathrm{always}\:\mathrm{has}\:\mathrm{got} \\ $$$$\mathrm{2}\:\mathrm{real}\:\mathrm{solutions}.\:\mathrm{but}\:\mathrm{to}\:\mathrm{generally}\:\mathrm{get}\:\mathrm{them} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{Ferrari}'\mathrm{s}\:\mathrm{Formula}\:\left(\mathrm{the}\:\mathrm{nasty}\:\mathrm{one}\right) \\ $$
