Menu Close

Question-166617

Tinku Tara 0 Comments
Pin




Question Number 166617 by mr W last updated on 23/Feb/22
Commented by mr W last updated on 23/Feb/22
three circles with radii a, b, c touch each other as shown. find the maximum side length of the equilateral triangle whose vertices lie on the three circles.
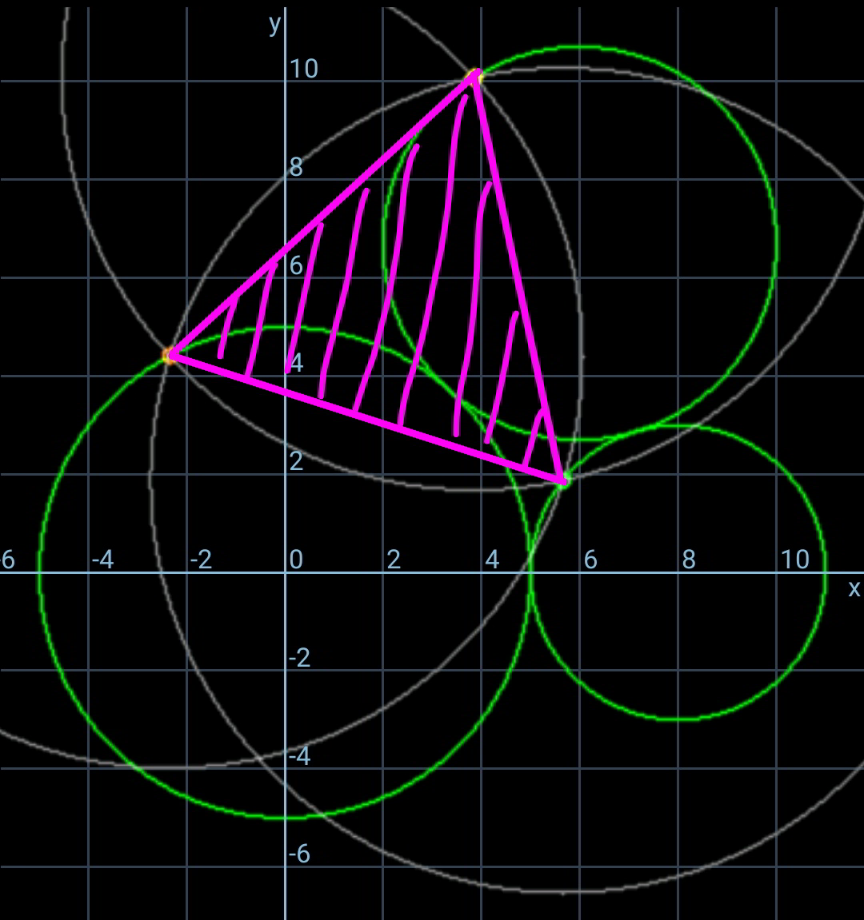
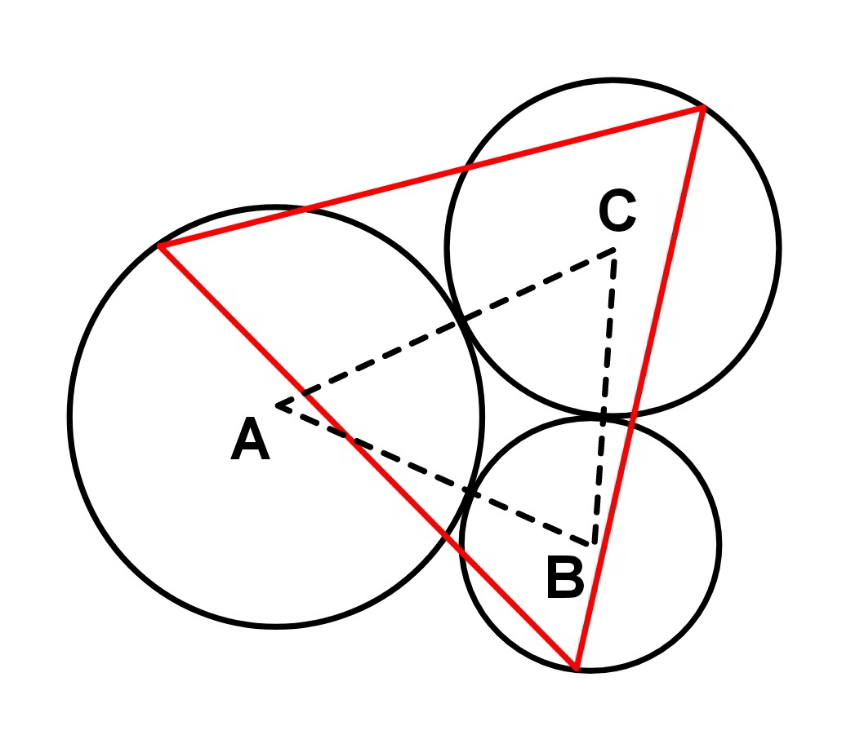
$${three}\:{circles}\:{with}\:{radii}\:{a},\:{b},\:{c}\: \\ $$$${touch}\:{each}\:{other}\:{as}\:{shown}.\: \\ $$$${find}\:{the}\:{maximum}\:{side}\:{length}\:{of}\: \\ $$$${the}\:{equilateral}\:{triangle}\:{whose}\: \\ $$$${vertices}\:{lie}\:{on}\:{the}\:{three}\:{circles}. \\ $$
Answered by ajfour last updated on 25/Feb/22
Answered by mr W last updated on 20/Mar/22
Commented by mr W last updated on 22/Mar/22
area of ABC Δ=(√(abc(a+b+c))) incircle radius r=(Δ/(a+b+c))=(√((abc)/(a+b+c))) α′=2 tan^(−1) (r/a) β′=2 tan^(−1) (r/b) γ′=2 tan^(−1) (r/c) PQ=s: s^2 =[a+b+a cos (α+α′)+b cos β]^2 +[a sin (α+α′)+b sin β]^2 s^2 =(a+b)^2 +a^2 +b^2 +2a(a+b)cos (α+α′)+2b(a+b) cos β+2ab[cos (α+α′)cos β+ sin (α+α′) sin β] (s^2 /2)−(a^2 +b^2 +ab)=(a+b)[a cos (α+α′)+b cos β]+ab[cos (α+α′)cos β+ sin (α+α′) sin β] (s^2 /2)−(a^2 +b^2 +ab)−a(a+b)cos (α+α′)=b{[a+b+a cos (α+α′)]cos β+a sin (α+α′) sin β} (s^2 /2)−(a^2 +b^2 +ab)−a(a+b)cos (α+α′)=b(√((a+b)^2 +a^2 +2a(a+b)cos (α+α′))) sin [β+tan^(−1) ((a+b+a cos (α+α′))/(a sin (α+α′)))] determinant (((β=−tan^(−1) ((a+b+a cos (α+α′))/(a sin (α+α′)))+sin^(−1) (((s^2 /2)−(a^2 +b^2 +ab)−a(a+b)cos (α+α′))/(b(√((a+b)^2 +a^2 +2a(a+b)cos (α+α′))))) ))) similarly RP=s: (s^2 /2)−(c^2 +a^2 +ca)=(c+a)[c cos (γ+γ′)+a cos α]+ca[cos (γ+γ′)cos α+ sin (γ+γ′) sin α] (s^2 /2)−(c^2 +a^2 +ca)−a(c+a)cos α=c{(c+a+a cos α) cos (γ+γ′)+a sin (γ+γ′) sin α} (s^2 /2)−(c^2 +a^2 +ca)−a(c+a)cos α=c(√((c+a)^2 +a^2 +2a(c+a)cos α)) sin (γ+γ′+tan^(−1) ((c+a+a cos α)/(a sin α))) determinant (((γ=−γ′−tan^(−1) ((c+a+a cos α)/(a sin α))+sin^(−1) (((s^2 /2)−(c^2 +a^2 +ca)−a(c+a)cos α)/(c(√((c+a)^2 +a^2 +2a(c+a)cos α))))))) similarly QR=s: (s^2 /2)−(b^2 +c^2 +bc)=(b+c)[b cos (β+β′)+c cos γ]+bc cos (β+β′−γ) determinant ((((s^2 /(2bc))−((b/c)+(c/b)+1)=(b+c)[((cos (β+β′))/c)+((cos γ)/b)]+cos (β+β′−γ))))
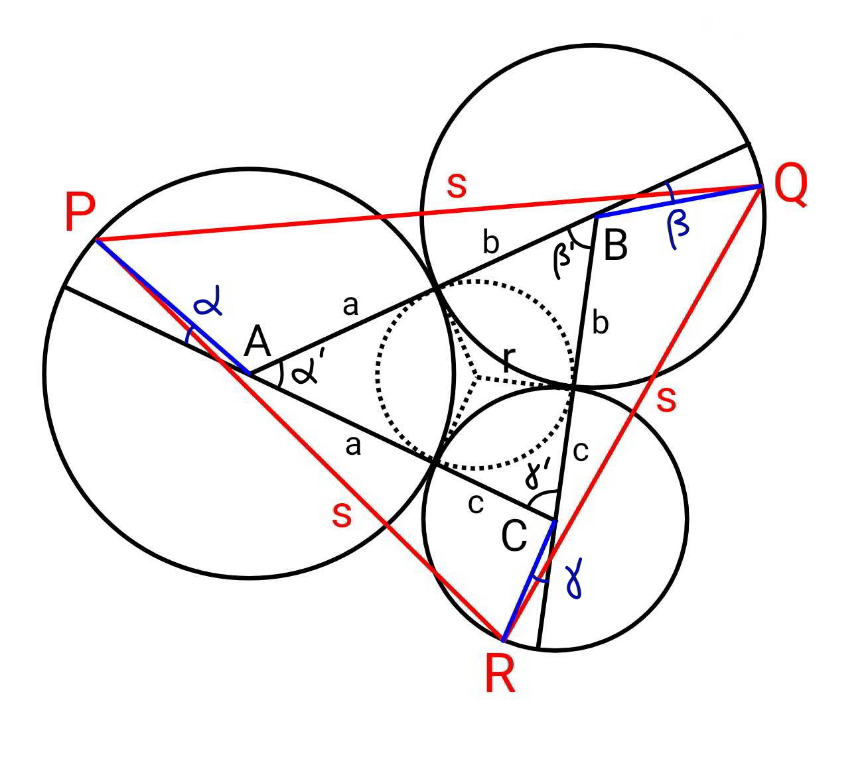
$${area}\:{of}\:{ABC}\:\Delta=\sqrt{{abc}\left({a}+{b}+{c}\right)} \\ $$$${incircle}\:{radius}\:{r}=\frac{\Delta}{{a}+{b}+{c}}=\sqrt{\frac{{abc}}{{a}+{b}+{c}}} \\ $$$$\alpha'=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{{r}}{{a}} \\ $$$$\beta'=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{{r}}{{b}} \\ $$$$\gamma'=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{{r}}{{c}} \\ $$$${PQ}={s}: \\ $$$${s}^{\mathrm{2}} =\left[{a}+{b}+{a}\:\mathrm{cos}\:\left(\alpha+\alpha'\right)+{b}\:\mathrm{cos}\:\beta\right]^{\mathrm{2}} +\left[{a}\:\mathrm{sin}\:\left(\alpha+\alpha'\right)+{b}\:\mathrm{sin}\:\beta\right]^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\alpha+\alpha'\right)+\mathrm{2}{b}\left({a}+{b}\right)\:\mathrm{cos}\:\beta+\mathrm{2}{ab}\left[\mathrm{cos}\:\left(\alpha+\alpha'\right)\mathrm{cos}\:\beta+\:\mathrm{sin}\:\left(\alpha+\alpha'\right)\:\mathrm{sin}\:\beta\right] \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)=\left({a}+{b}\right)\left[{a}\:\mathrm{cos}\:\left(\alpha+\alpha'\right)+{b}\:\mathrm{cos}\:\beta\right]+{ab}\left[\mathrm{cos}\:\left(\alpha+\alpha'\right)\mathrm{cos}\:\beta+\:\mathrm{sin}\:\left(\alpha+\alpha'\right)\:\mathrm{sin}\:\beta\right] \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)−{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\alpha+\alpha'\right)={b}\left\{\left[{a}+{b}+{a}\:\mathrm{cos}\:\left(\alpha+\alpha'\right)\right]\mathrm{cos}\:\beta+{a}\:\mathrm{sin}\:\left(\alpha+\alpha'\right)\:\mathrm{sin}\:\beta\right\} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)−{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\alpha+\alpha'\right)={b}\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\alpha+\alpha'\right)}\:\mathrm{sin}\:\left[\beta+\mathrm{tan}^{−\mathrm{1}} \frac{{a}+{b}+{a}\:\mathrm{cos}\:\left(\alpha+\alpha'\right)}{{a}\:\mathrm{sin}\:\left(\alpha+\alpha'\right)}\right] \\ $$$$\begin{array}{|c|}{\beta=−\mathrm{tan}^{−\mathrm{1}} \frac{{a}+{b}+{a}\:\mathrm{cos}\:\left(\alpha+\alpha'\right)}{{a}\:\mathrm{sin}\:\left(\alpha+\alpha'\right)}+\mathrm{sin}^{−\mathrm{1}} \frac{\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}\right)−{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\alpha+\alpha'\right)}{{b}\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{a}\left({a}+{b}\right)\mathrm{cos}\:\left(\alpha+\alpha'\right)}}\:}\\\hline\end{array} \\ $$$${similarly} \\ $$$${RP}={s}: \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{ca}\right)=\left({c}+{a}\right)\left[{c}\:\mathrm{cos}\:\left(\gamma+\gamma'\right)+{a}\:\mathrm{cos}\:\alpha\right]+{ca}\left[\mathrm{cos}\:\left(\gamma+\gamma'\right)\mathrm{cos}\:\alpha+\:\mathrm{sin}\:\left(\gamma+\gamma'\right)\:\mathrm{sin}\:\alpha\right] \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{ca}\right)−{a}\left({c}+{a}\right)\mathrm{cos}\:\alpha={c}\left\{\left({c}+{a}+{a}\:\mathrm{cos}\:\alpha\right)\:\mathrm{cos}\:\left(\gamma+\gamma'\right)+{a}\:\mathrm{sin}\:\left(\gamma+\gamma'\right)\:\mathrm{sin}\:\alpha\right\} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{ca}\right)−{a}\left({c}+{a}\right)\mathrm{cos}\:\alpha={c}\sqrt{\left({c}+{a}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{a}\left({c}+{a}\right)\mathrm{cos}\:\alpha}\:\mathrm{sin}\:\left(\gamma+\gamma'+\mathrm{tan}^{−\mathrm{1}} \frac{{c}+{a}+{a}\:\mathrm{cos}\:\alpha}{{a}\:\mathrm{sin}\:\alpha}\right) \\ $$$$\begin{array}{|c|}{\gamma=−\gamma'−\mathrm{tan}^{−\mathrm{1}} \frac{{c}+{a}+{a}\:\mathrm{cos}\:\alpha}{{a}\:\mathrm{sin}\:\alpha}+\mathrm{sin}^{−\mathrm{1}} \frac{\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{ca}\right)−{a}\left({c}+{a}\right)\mathrm{cos}\:\alpha}{{c}\sqrt{\left({c}+{a}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{a}\left({c}+{a}\right)\mathrm{cos}\:\alpha}}}\\\hline\end{array} \\ $$$${similarly} \\ $$$${QR}={s}: \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\right)=\left({b}+{c}\right)\left[{b}\:\mathrm{cos}\:\left(\beta+\beta'\right)+{c}\:\mathrm{cos}\:\gamma\right]+{bc}\:\mathrm{cos}\:\left(\beta+\beta'−\gamma\right) \\ $$$$\begin{array}{|c|}{\frac{{s}^{\mathrm{2}} }{\mathrm{2}{bc}}−\left(\frac{{b}}{{c}}+\frac{{c}}{{b}}+\mathrm{1}\right)=\left({b}+{c}\right)\left[\frac{\mathrm{cos}\:\left(\beta+\beta'\right)}{{c}}+\frac{\mathrm{cos}\:\gamma}{{b}}\right]+\mathrm{cos}\:\left(\beta+\beta'−\gamma\right)}\\\hline\end{array} \\ $$
Commented by mr W last updated on 20/Mar/22

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *