Question Number 166649 by kurt last updated on 24/Feb/22
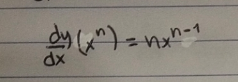
Commented by greogoury55 last updated on 27/Feb/22
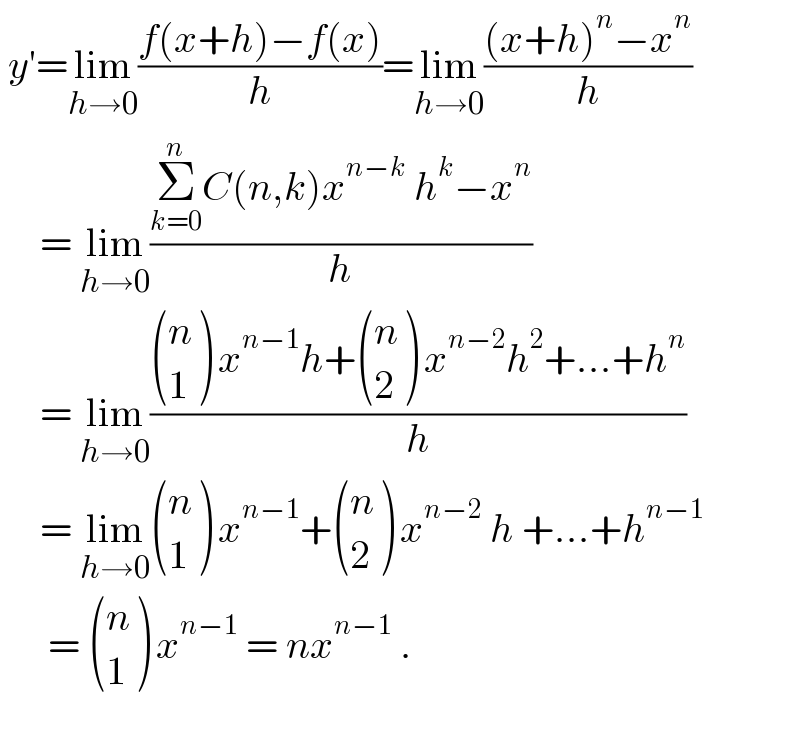
$$\:{y}'=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}}=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}+{h}\right)^{{n}} −{x}^{{n}} }{{h}} \\ $$$$\:\:\:\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}\left({n},{k}\right){x}^{{n}−{k}} \:{h}^{{k}} −{x}^{{n}} }{{h}} \\ $$$$\:\:\:\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:{x}^{{n}−\mathrm{1}} {h}+\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:{x}^{{n}−\mathrm{2}} {h}^{\mathrm{2}} +…+{h}^{{n}} }{{h}} \\ $$$$\:\:\:\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:{x}^{{n}−\mathrm{1}} +\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:{x}^{{n}−\mathrm{2}} \:{h}\:+…+{h}^{{n}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:=\:\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:{x}^{{n}−\mathrm{1}} \:=\:{nx}^{{n}−\mathrm{1}} \:. \\ $$$$ \\ $$
