Question-166738

Question Number 166738 by ajfour last updated on 26/Feb/22

Commented by ajfour last updated on 26/Feb/22

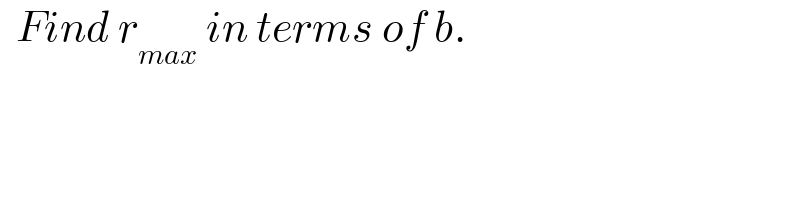
$$\:\:{Find}\:{r}_{{max}} \:{in}\:{terms}\:{of}\:{b}. \\ $$

Answered by mr W last updated on 27/Feb/22

P(a cos θ, b sin θ) ((√((b sin θ−r)^2 −r^2 ))/r)=((b sin θ)/(a cos θ)) let (b/a)=μ≤1, (b/r)=ξ (√((ξ sin θ−1)^2 −1))=((μ sin θ)/(cos θ)) ξ=(1/(sin θ))(1+(√((μ^2 /((1/(sin^2 θ))−1))+1))) let s=(1/(sin θ)) ξ=s(1+(√((μ^2 /(s^2 −1))+1))) (dξ/ds)=1+(√((μ^2 /(s^2 −1))+1))−((μ^2 s^2 )/( (s^2 −1)^2 (√((μ^2 /(s^2 −1))+1))))=0 (s^2 −1)^2 +(√((μ^2 /(s^2 −1))+1))=μ^2 (√((μ^2 /(s^2 −1))+1))=((μ/(s^2 −1)))^2 −1 ((μ/(s^2 −1)))^3 −2((μ/(s^2 −1)))−μ=0 Δ=(μ^2 /4)−(8/(27))≤(1/4)−(8/(27))=−(5/(108))<0 (μ/(s^2 −1))=((2(√6))/3) sin ((π/3)+(1/3)sin^(−1) ((3(√6)μ)/8)) (valid for μ≤(√((32 )/(27)))=((4(√6))/9)) if μ>((4(√6))/9), (μ/(s^2 −1))=(((√((μ^2 /4)−(8/(27))))+(μ/2)))^(1/3) −(((√((μ^2 /4)−(8/(27))))−(μ/2)))^(1/3) s=(1/(sin θ))=(√(1+(((√6)μ)/(4 sin ((π/3)+(1/3)sin^(−1) ((3(√6)μ)/8)))))) for μ≤((4(√6))/9) s=(1/(sin θ))=(√(1+(μ/( (((√((μ^2 /4)−(8/(27))))+(μ/2)))^(1/3) −(((√((μ^2 /4)−(8/(27))))−(μ/2)))^(1/3) )))) for μ<((4(√6))/9) ξ_(min) =(b/r_(max) )=s(1+(√((μ^2 /(s^2 −1))+1))) examples: μ=(b/a)=0.5 ⇒ (r_(max) /b)≈0.3728 μ=(b/a)=2 ⇒ (r_(max) /b)≈0.1987

$${P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\frac{\sqrt{\left({b}\:\mathrm{sin}\:\theta−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }}{{r}}=\frac{{b}\:\mathrm{sin}\:\theta}{{a}\:\mathrm{cos}\:\theta} \\ $$$${let}\:\frac{{b}}{{a}}=\mu\leqslant\mathrm{1},\:\frac{{b}}{{r}}=\xi \\ $$$$\sqrt{\left(\xi\:\mathrm{sin}\:\theta−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}=\frac{\mu\:\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$\xi=\frac{\mathrm{1}}{\mathrm{sin}\:\theta}\left(\mathrm{1}+\sqrt{\frac{\mu^{\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\theta}−\mathrm{1}}+\mathrm{1}}\right) \\ $$$${let}\:{s}=\frac{\mathrm{1}}{\mathrm{sin}\:\theta} \\ $$$$\xi={s}\left(\mathrm{1}+\sqrt{\frac{\mu^{\mathrm{2}} }{{s}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}}\right) \\ $$$$\frac{{d}\xi}{{ds}}=\mathrm{1}+\sqrt{\frac{\mu^{\mathrm{2}} }{{s}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}}−\frac{\mu^{\mathrm{2}} {s}^{\mathrm{2}} }{\:\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\mu^{\mathrm{2}} }{{s}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}}}=\mathrm{0} \\ $$$$\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\sqrt{\frac{\mu^{\mathrm{2}} }{{s}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}}=\mu^{\mathrm{2}} \\ $$$$\sqrt{\frac{\mu^{\mathrm{2}} }{{s}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}}=\left(\frac{\mu}{{s}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\left(\frac{\mu}{{s}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{3}} −\mathrm{2}\left(\frac{\mu}{{s}^{\mathrm{2}} −\mathrm{1}}\right)−\mu=\mathrm{0} \\ $$$$\Delta=\frac{\mu^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{27}}\leqslant\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{27}}=−\frac{\mathrm{5}}{\mathrm{108}}<\mathrm{0} \\ $$$$\frac{\mu}{{s}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{6}}\mu}{\mathrm{8}}\right)\:\left({valid}\:{for}\:\mu\leqslant\sqrt{\frac{\mathrm{32}\:}{\mathrm{27}}}=\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{9}}\right) \\ $$$${if}\:\mu>\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{9}},\: \\ $$$$\frac{\mu}{{s}^{\mathrm{2}} −\mathrm{1}}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mu^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{27}}}+\frac{\mu}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mu^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{27}}}−\frac{\mu}{\mathrm{2}}} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{sin}\:\theta}=\sqrt{\mathrm{1}+\frac{\sqrt{\mathrm{6}}\mu}{\mathrm{4}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{6}}\mu}{\mathrm{8}}\right)}}\:\:{for}\:\mu\leqslant\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{9}} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{sin}\:\theta}=\sqrt{\mathrm{1}+\frac{\mu}{\:\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mu^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{27}}}+\frac{\mu}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mu^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{8}}{\mathrm{27}}}−\frac{\mu}{\mathrm{2}}}}}\:\:{for}\:\mu<\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{9}} \\ $$$$\xi_{{min}} =\frac{{b}}{{r}_{{max}} }={s}\left(\mathrm{1}+\sqrt{\frac{\mu^{\mathrm{2}} }{{s}^{\mathrm{2}} −\mathrm{1}}+\mathrm{1}}\right) \\ $$$$ \\ $$$${examples}: \\ $$$$\mu=\frac{{b}}{{a}}=\mathrm{0}.\mathrm{5}\:\Rightarrow\:\frac{{r}_{{max}} }{{b}}\approx\mathrm{0}.\mathrm{3728} \\ $$$$\mu=\frac{{b}}{{a}}=\mathrm{2}\:\Rightarrow\:\frac{{r}_{{max}} }{{b}}\approx\mathrm{0}.\mathrm{1987} \\ $$

Commented by mr W last updated on 27/Feb/22

Commented by mr W last updated on 27/Feb/22

Commented by mr W last updated on 27/Feb/22

Commented by ajfour last updated on 27/Feb/22

$${Great}\:{effort}\:{n}\:{solution}\:{Sir}. \\ $$$${Thanks}\:{a}\:{lot}. \\ $$

Answered by ajfour last updated on 26/Feb/22

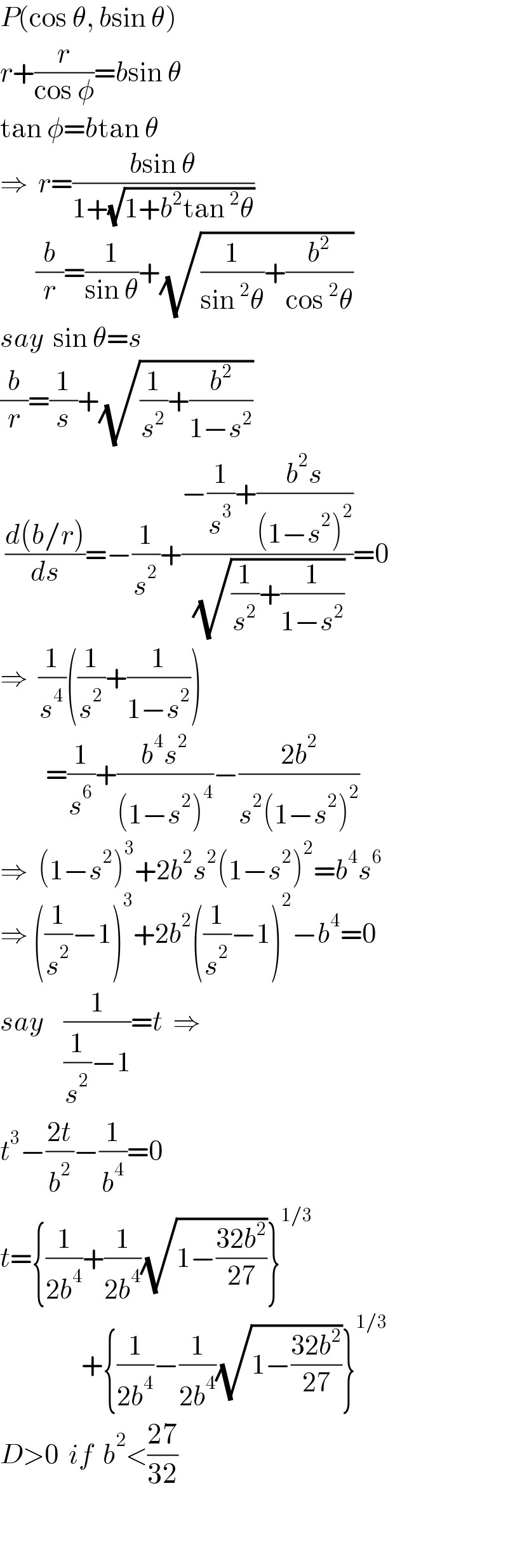
P(cos θ, bsin θ) r+(r/(cos φ))=bsin θ tan φ=btan θ ⇒ r=((bsin θ)/(1+(√(1+b^2 tan^2 θ)))) (b/r)=(1/(sin θ))+(√((1/(sin^2 θ))+(b^2 /(cos^2 θ)))) say sin θ=s (b/r)=(1/s)+(√((1/s^2 )+(b^2 /(1−s^2 )))) ((d(b/r))/ds)=−(1/s^2 )+((−(1/s^3 )+((b^2 s)/((1−s^2 )^2 )))/( (√((1/s^2 )+(1/(1−s^2 ))))))=0 ⇒ (1/s^4 )((1/s^2 )+(1/(1−s^2 ))) =(1/s^6 )+((b^4 s^2 )/((1−s^2 )^4 ))−((2b^2 )/(s^2 (1−s^2 )^2 )) ⇒ (1−s^2 )^3 +2b^2 s^2 (1−s^2 )^2 =b^4 s^6 ⇒ ((1/s^2 )−1)^3 +2b^2 ((1/s^2 )−1)^2 −b^4 =0 say (1/((1/s^2 )−1))=t ⇒ t^3 −((2t)/b^2 )−(1/b^4 )=0 t={(1/(2b^4 ))+(1/(2b^4 ))(√(1−((32b^2 )/(27))))}^(1/3) +{(1/(2b^4 ))−(1/(2b^4 ))(√(1−((32b^2 )/(27))))}^(1/3) D>0 if b^2 <((27)/(32))

$${P}\left(\mathrm{cos}\:\theta,\:{b}\mathrm{sin}\:\theta\right) \\ $$$${r}+\frac{{r}}{\mathrm{cos}\:\phi}={b}\mathrm{sin}\:\theta \\ $$$$\mathrm{tan}\:\phi={b}\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:{r}=\frac{{b}\mathrm{sin}\:\theta}{\mathrm{1}+\sqrt{\mathrm{1}+{b}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta}} \\ $$$$\:\:\:\:\:\:\:\frac{{b}}{{r}}=\frac{\mathrm{1}}{\mathrm{sin}\:\theta}+\sqrt{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \theta}+\frac{{b}^{\mathrm{2}} }{\mathrm{cos}\:^{\mathrm{2}} \theta}} \\ $$$${say}\:\:\mathrm{sin}\:\theta={s} \\ $$$$\frac{{b}}{{r}}=\frac{\mathrm{1}}{{s}}+\sqrt{\frac{\mathrm{1}}{{s}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{\mathrm{1}−{s}^{\mathrm{2}} }} \\ $$$$\:\frac{{d}\left({b}/{r}\right)}{{ds}}=−\frac{\mathrm{1}}{{s}^{\mathrm{2}} }+\frac{−\frac{\mathrm{1}}{{s}^{\mathrm{3}} }+\frac{{b}^{\mathrm{2}} {s}}{\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\:\sqrt{\frac{\mathrm{1}}{{s}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}−{s}^{\mathrm{2}} }}}=\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{{s}^{\mathrm{4}} }\left(\frac{\mathrm{1}}{{s}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}−{s}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{s}^{\mathrm{6}} }+\frac{{b}^{\mathrm{4}} {s}^{\mathrm{2}} }{\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{4}} }−\frac{\mathrm{2}{b}^{\mathrm{2}} }{{s}^{\mathrm{2}} \left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{2}{b}^{\mathrm{2}} {s}^{\mathrm{2}} \left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{2}} ={b}^{\mathrm{4}} {s}^{\mathrm{6}} \\ $$$$\Rightarrow\:\left(\frac{\mathrm{1}}{{s}^{\mathrm{2}} }−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{2}{b}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{s}^{\mathrm{2}} }−\mathrm{1}\right)^{\mathrm{2}} −{b}^{\mathrm{4}} =\mathrm{0} \\ $$$${say}\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{{s}^{\mathrm{2}} }−\mathrm{1}}={t}\:\:\Rightarrow \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{2}{t}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{b}^{\mathrm{4}} }=\mathrm{0} \\ $$$${t}=\left\{\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{4}} }\sqrt{\mathrm{1}−\frac{\mathrm{32}{b}^{\mathrm{2}} }{\mathrm{27}}}\right\}^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left\{\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{2}{b}^{\mathrm{4}} }\sqrt{\mathrm{1}−\frac{\mathrm{32}{b}^{\mathrm{2}} }{\mathrm{27}}}\right\}^{\mathrm{1}/\mathrm{3}} \\ $$$${D}>\mathrm{0}\:\:{if}\:\:{b}^{\mathrm{2}} <\frac{\mathrm{27}}{\mathrm{32}} \\ $$$$ \\ $$$$ \\ $$

Answered by MJS_new last updated on 27/Feb/22

for 0≤x≤1 and the triangle has the sides u, v, w u=v=(√(b^2 +(1−b^2 )x^2 )) and w=2x ⇒ the radius of the incircle is r=((bx(√(1−x^2 )))/(x+(√(b^2 +(1−b^2 )x^2 )))) r′=0 ⇔ (1−b^2 )x^4 −2(1−b^2 )x^2 −b^2 =x(x^2 −2)(√(b^2 +(1−b^2 )x^2 )) (obviously this is always true for x=1) squaring both sides and transforming we get (x^2 −1)(x^6 −((2−3b^2 )/(1−b^2 ))x^4 −((3b^2 x^2 )/(1−b^2 ))+(b^2 /(1−b^2 )))=0 and we can always find an exact solution for any given b with x=(√y)∧y=z+((2−3b^2 )/(3(1−b^2 ))) and z^3 −((4−3b^2 )/(3(1−b^2 )^2 ))z−((16−45b^2 +27b^4 )/(27(1−b^2 )^3 ))=0 ⇒ 0<b<1∨1<b<((4(√6))/9) z=−((2(√(4−3b^2 )))/(3(1−b^2 )))sin ((1/3)arcsin ((16−45b^2 +27b^4 )/(2(4−3b^2 )^(3/2) ))) b=1 r′ reduces to x^3 −2x+1=0 ⇒ x=−(1/2)+((√5)/2) ((4(√6))/9)≤b<((2(√3))/3)∨b>((2(√3))/3) we get z with Cardano′s Formula b=((2(√3))/3) z^3 +4=0 ⇒ z=−2^(2/3)

$$\mathrm{for}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\mathrm{and}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{has}\:\mathrm{the} \\ $$$$\mathrm{sides}\:{u},\:{v},\:{w} \\ $$$${u}={v}=\sqrt{{b}^{\mathrm{2}} +\left(\mathrm{1}−{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} }\:\mathrm{and}\:{w}=\mathrm{2}{x} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{incircle}\:\mathrm{is} \\ $$$${r}=\frac{{bx}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}+\sqrt{{b}^{\mathrm{2}} +\left(\mathrm{1}−{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} }} \\ $$$${r}'=\mathrm{0}\:\Leftrightarrow\:\left(\mathrm{1}−{b}^{\mathrm{2}} \right){x}^{\mathrm{4}} −\mathrm{2}\left(\mathrm{1}−{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} −{b}^{\mathrm{2}} ={x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)\sqrt{{b}^{\mathrm{2}} +\left(\mathrm{1}−{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{obviously}\:\mathrm{this}\:\mathrm{is}\:\mathrm{always}\:\mathrm{true}\:\mathrm{for}\:{x}=\mathrm{1}\right) \\ $$$$\mathrm{squaring}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{and}\:\mathrm{transforming}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{6}} −\frac{\mathrm{2}−\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{1}−{b}^{\mathrm{2}} }{x}^{\mathrm{4}} −\frac{\mathrm{3}{b}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{1}−{b}^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} }{\mathrm{1}−{b}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{always}\:\mathrm{find}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{solution} \\ $$$$\mathrm{for}\:\mathrm{any}\:\mathrm{given}\:{b}\:\mathrm{with} \\ $$$${x}=\sqrt{{y}}\wedge{y}={z}+\frac{\mathrm{2}−\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}−{b}^{\mathrm{2}} \right)} \\ $$$$\mathrm{and} \\ $$$${z}^{\mathrm{3}} −\frac{\mathrm{4}−\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{z}−\frac{\mathrm{16}−\mathrm{45}{b}^{\mathrm{2}} +\mathrm{27}{b}^{\mathrm{4}} }{\mathrm{27}\left(\mathrm{1}−{b}^{\mathrm{2}} \right)^{\mathrm{3}} }=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}<{b}<\mathrm{1}\vee\mathrm{1}<{b}<\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{9}} \\ $$$${z}=−\frac{\mathrm{2}\sqrt{\mathrm{4}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{3}\left(\mathrm{1}−{b}^{\mathrm{2}} \right)}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{16}−\mathrm{45}{b}^{\mathrm{2}} +\mathrm{27}{b}^{\mathrm{4}} }{\mathrm{2}\left(\mathrm{4}−\mathrm{3}{b}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\right) \\ $$$${b}=\mathrm{1} \\ $$$${r}'\:\mathrm{reduces}\:\mathrm{to}\:{x}^{\mathrm{3}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{9}}\leqslant{b}<\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\vee{b}>\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\mathrm{we}\:\mathrm{get}\:{z}\:\mathrm{with}\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{Formula} \\ $$$${b}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${z}^{\mathrm{3}} +\mathrm{4}=\mathrm{0}\:\Rightarrow\:{z}=−\mathrm{2}^{\mathrm{2}/\mathrm{3}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply