Question Number 166749 by Tawa11 last updated on 27/Feb/22

Commented by mr W last updated on 27/Feb/22
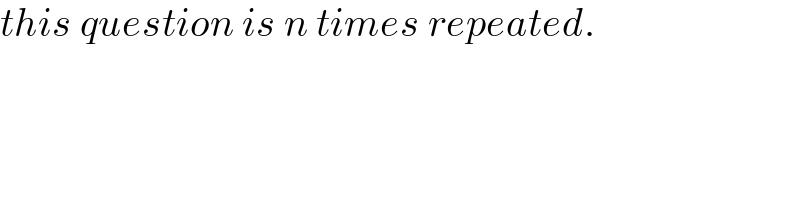
$${this}\:{question}\:{is}\:{n}\:{times}\:{repeated}. \\ $$
Answered by mr W last updated on 27/Feb/22

Commented by Tawa11 last updated on 27/Feb/22
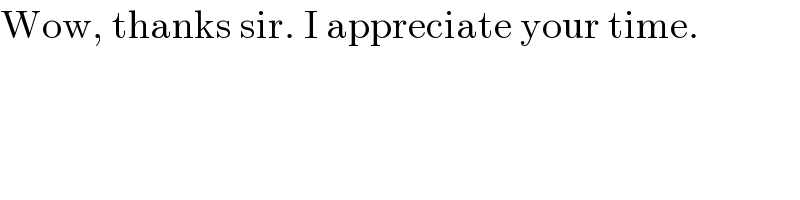
$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by mr W last updated on 27/Feb/22
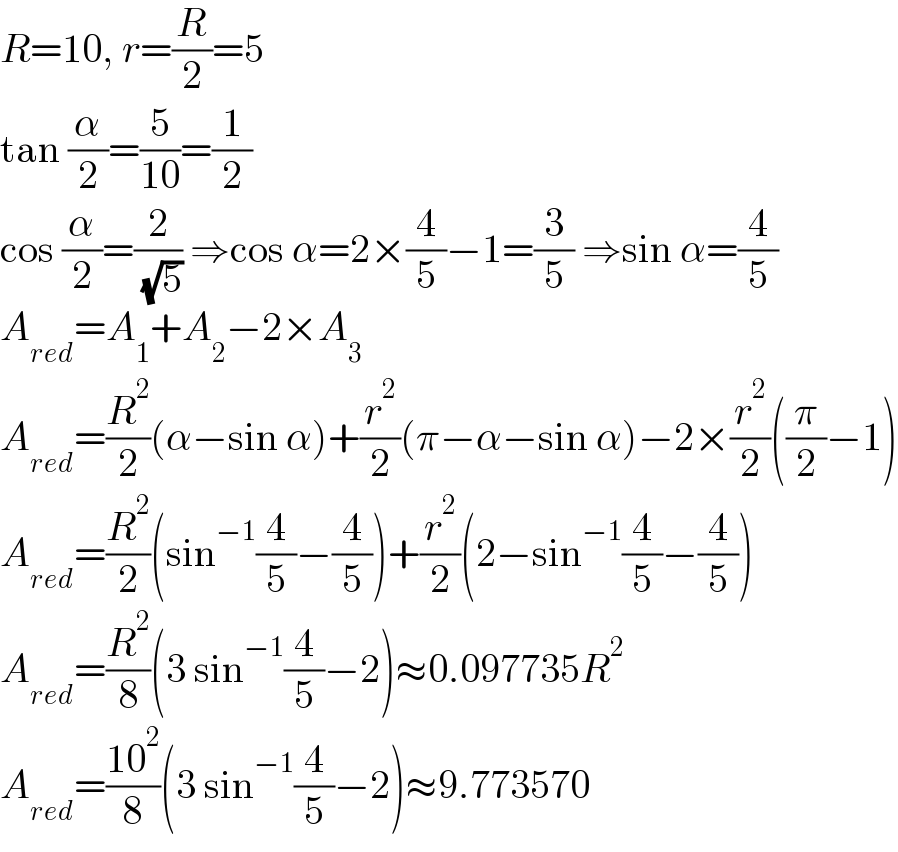
$${R}=\mathrm{10},\:{r}=\frac{{R}}{\mathrm{2}}=\mathrm{5} \\ $$$$\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\Rightarrow\mathrm{cos}\:\alpha=\mathrm{2}×\frac{\mathrm{4}}{\mathrm{5}}−\mathrm{1}=\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${A}_{{red}} ={A}_{\mathrm{1}} +{A}_{\mathrm{2}} −\mathrm{2}×{A}_{\mathrm{3}} \\ $$$${A}_{{red}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\mathrm{sin}\:\alpha\right)+\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\alpha−\mathrm{sin}\:\alpha\right)−\mathrm{2}×\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{1}\right) \\ $$$${A}_{{red}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{5}}\right)+\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$${A}_{{red}} =\frac{{R}^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{3}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{2}\right)\approx\mathrm{0}.\mathrm{097735}{R}^{\mathrm{2}} \\ $$$${A}_{{red}} =\frac{\mathrm{10}^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{3}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{2}\right)\approx\mathrm{9}.\mathrm{773570} \\ $$
Commented by mr W last updated on 27/Feb/22

Commented by mr W last updated on 27/Feb/22

