Question Number 166793 by leicianocosta last updated on 28/Feb/22
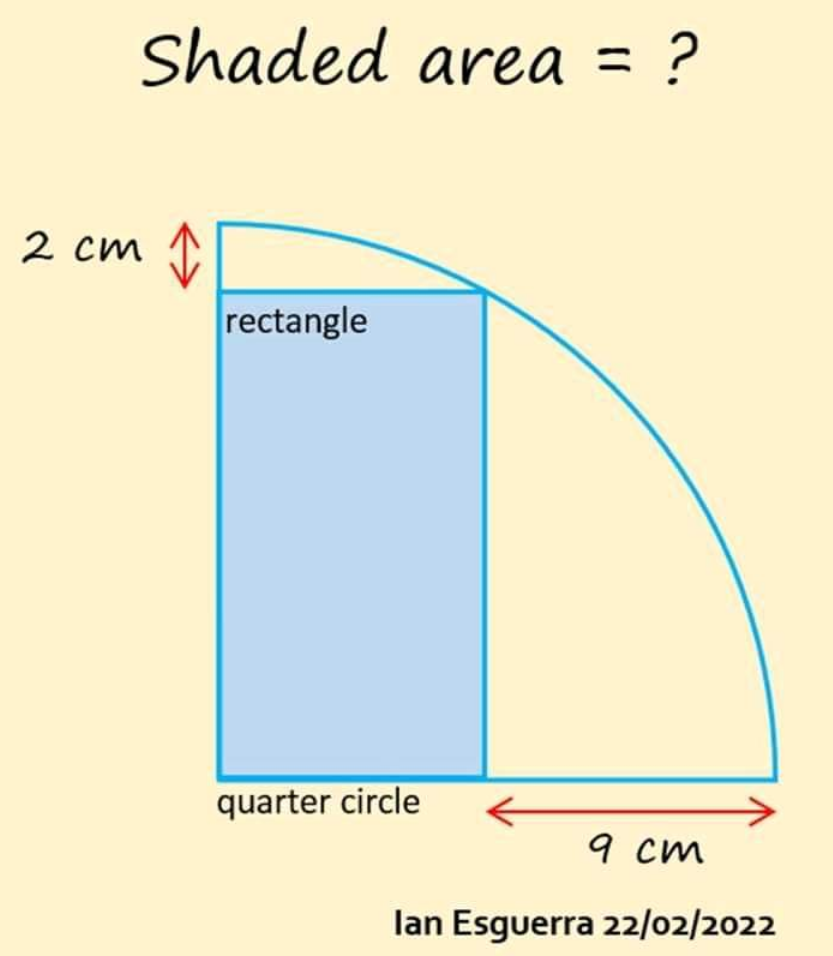
Answered by Rasheed.Sindhi last updated on 28/Feb/22
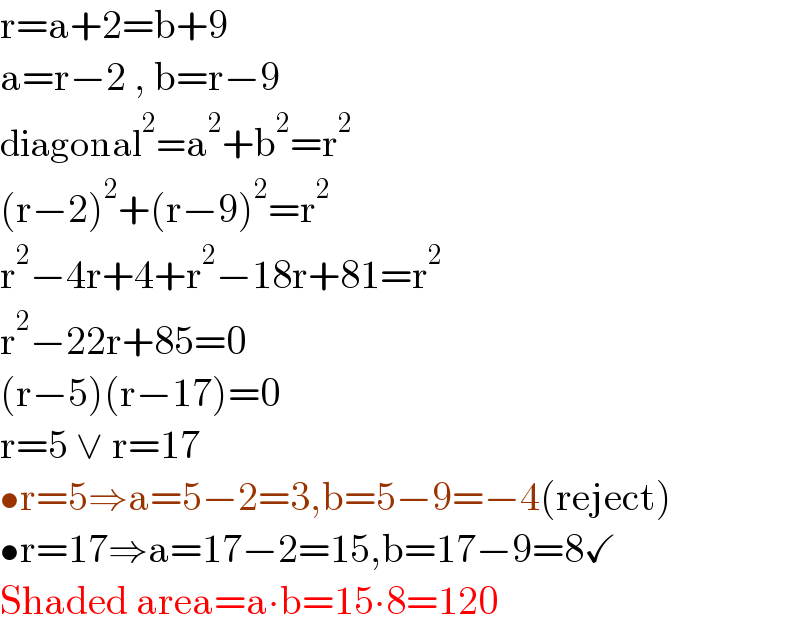
$$\mathrm{r}=\mathrm{a}+\mathrm{2}=\mathrm{b}+\mathrm{9} \\ $$$$\mathrm{a}=\mathrm{r}−\mathrm{2}\:,\:\mathrm{b}=\mathrm{r}−\mathrm{9} \\ $$$$\mathrm{diagonal}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \\ $$$$\left(\mathrm{r}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{r}−\mathrm{9}\right)^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \\ $$$$\mathrm{r}^{\mathrm{2}} −\mathrm{4r}+\mathrm{4}+\mathrm{r}^{\mathrm{2}} −\mathrm{18r}+\mathrm{81}=\mathrm{r}^{\mathrm{2}} \\ $$$$\mathrm{r}^{\mathrm{2}} −\mathrm{22r}+\mathrm{85}=\mathrm{0} \\ $$$$\left(\mathrm{r}−\mathrm{5}\right)\left(\mathrm{r}−\mathrm{17}\right)=\mathrm{0} \\ $$$$\mathrm{r}=\mathrm{5}\:\vee\:\mathrm{r}=\mathrm{17} \\ $$$$\bullet\mathrm{r}=\mathrm{5}\Rightarrow\mathrm{a}=\mathrm{5}−\mathrm{2}=\mathrm{3},\mathrm{b}=\mathrm{5}−\mathrm{9}=−\mathrm{4}\left(\mathrm{reject}\right) \\ $$$$\bullet\mathrm{r}=\mathrm{17}\Rightarrow\mathrm{a}=\mathrm{17}−\mathrm{2}=\mathrm{15},\mathrm{b}=\mathrm{17}−\mathrm{9}=\mathrm{8}\checkmark \\ $$$$\mathrm{Shaded}\:\mathrm{area}=\mathrm{a}\centerdot\mathrm{b}=\mathrm{15}\centerdot\mathrm{8}=\mathrm{120} \\ $$
Commented by Tawa11 last updated on 03/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
