Question Number 166861 by Tawa11 last updated on 01/Mar/22
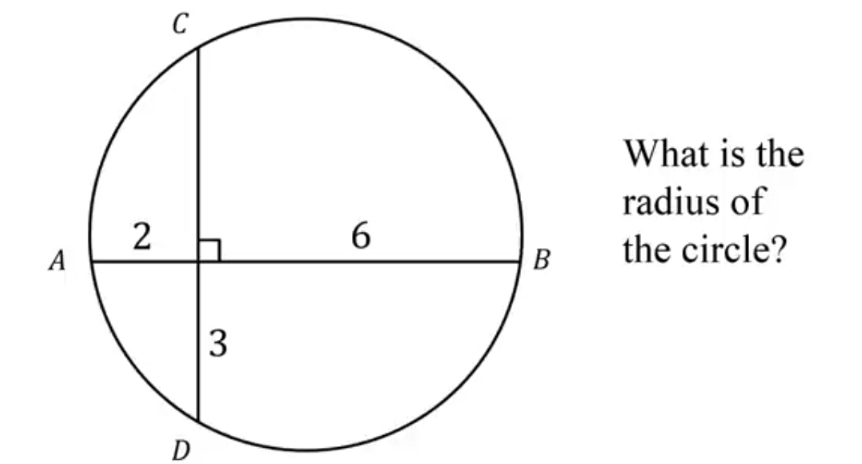
Commented by cortano1 last updated on 01/Mar/22
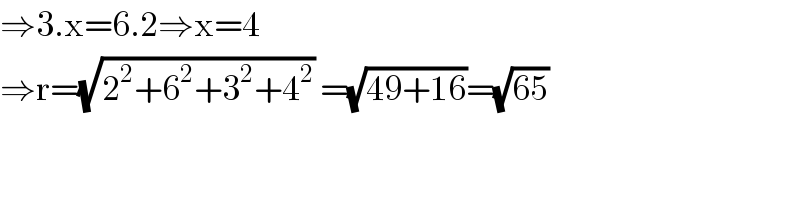
$$\Rightarrow\mathrm{3}.\mathrm{x}=\mathrm{6}.\mathrm{2}\Rightarrow\mathrm{x}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{r}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }\:=\sqrt{\mathrm{49}+\mathrm{16}}=\sqrt{\mathrm{65}} \\ $$
Commented by mr W last updated on 01/Mar/22

$${wrong}. \\ $$$${r}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$
Commented by cortano1 last updated on 01/Mar/22

$$\mathrm{AB}\:\mathrm{not}\:\mathrm{diameter} \\ $$
Commented by cortano1 last updated on 01/Mar/22

Commented by mr W last updated on 01/Mar/22
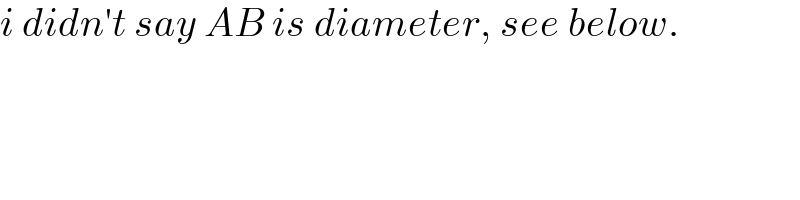
$${i}\:{didn}'{t}\:{say}\:{AB}\:{is}\:{diameter},\:{see}\:{below}. \\ $$
Commented by mr W last updated on 01/Mar/22

$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={R}^{\mathrm{2}} \:{is}\:{correct},\:{but}\:{it} \\ $$$${is}\:{also}\:{said}\:\left({in}\:{Japanese}\right)\:{that}\:{R} \\ $$$${is}\:{the}\:{diameter}\:{of}\:{the}\:{circle}. \\ $$
Commented by Tawa11 last updated on 01/Mar/22

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by TheSupreme last updated on 01/Mar/22
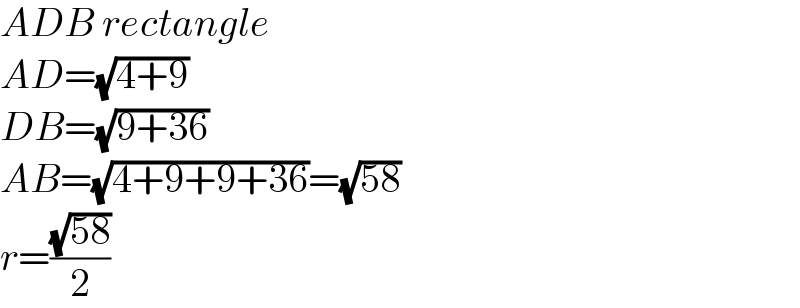
$${ADB}\:{rectangle} \\ $$$${AD}=\sqrt{\mathrm{4}+\mathrm{9}} \\ $$$${DB}=\sqrt{\mathrm{9}+\mathrm{36}} \\ $$$${AB}=\sqrt{\mathrm{4}+\mathrm{9}+\mathrm{9}+\mathrm{36}}=\sqrt{\mathrm{58}} \\ $$$${r}=\frac{\sqrt{\mathrm{58}}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 01/Mar/22

$${wrong}. \\ $$$${how}\:{are}\:{you}\:{sure}\:{that}\:\angle{ADB}\:{is}\: \\ $$$${rectangle}\:{and}\:{AB}\:{is}\:{diameter}? \\ $$$${if}\:{AB}\:{were}\:{diameter}\:{and}\:\angle{ADB} \\ $$$${were}\:{rectangle},\:{then}\:{you}\:{should} \\ $$$${have}\:\mathrm{2}×\mathrm{6}=\mathrm{3}^{\mathrm{2}} ,\:{but}\:{this}\:{is}\:{not}\:{sure}, \\ $$$${therefore}\:{AB}\:{is}\:{not}\:{diameter}\:{and} \\ $$$$\angle{ADB}\:{is}\:{not}\:{rectangle}. \\ $$
Answered by mr W last updated on 01/Mar/22

Commented by mr W last updated on 01/Mar/22
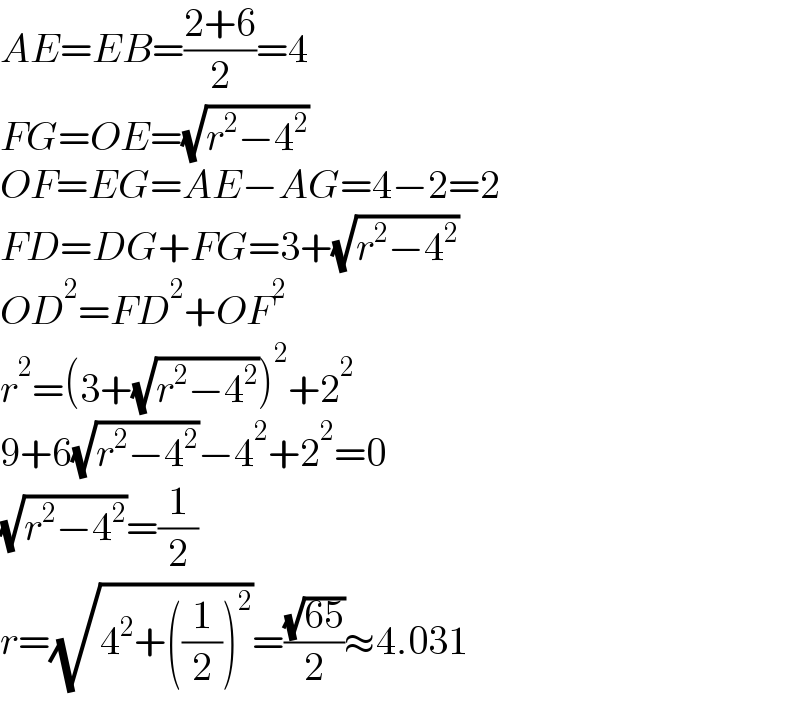
$${AE}={EB}=\frac{\mathrm{2}+\mathrm{6}}{\mathrm{2}}=\mathrm{4} \\ $$$${FG}={OE}=\sqrt{{r}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} } \\ $$$${OF}={EG}={AE}−{AG}=\mathrm{4}−\mathrm{2}=\mathrm{2} \\ $$$${FD}={DG}+{FG}=\mathrm{3}+\sqrt{{r}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} } \\ $$$${OD}^{\mathrm{2}} ={FD}^{\mathrm{2}} +{OF}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} =\left(\mathrm{3}+\sqrt{{r}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{9}+\mathrm{6}\sqrt{{r}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }−\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} =\mathrm{0} \\ $$$$\sqrt{{r}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${r}=\sqrt{\mathrm{4}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}}\approx\mathrm{4}.\mathrm{031} \\ $$
Commented by Tawa11 last updated on 01/Mar/22
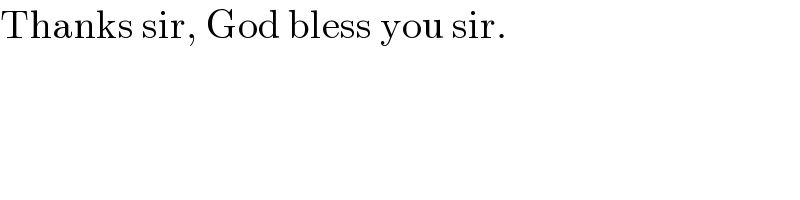
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by MJS_new last updated on 04/Mar/22
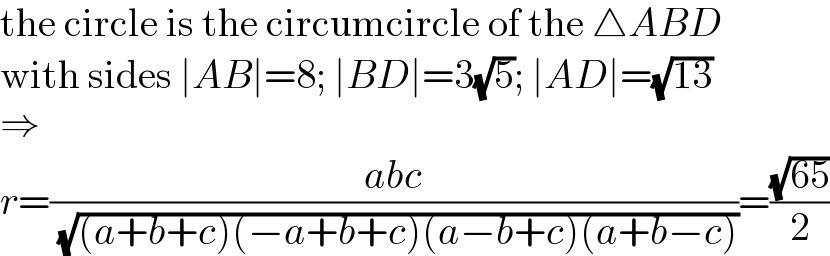
$$\mathrm{the}\:\mathrm{circle}\:\mathrm{is}\:\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{of}\:\mathrm{the}\:\bigtriangleup{ABD} \\ $$$$\mathrm{with}\:\mathrm{sides}\:\mid{AB}\mid=\mathrm{8};\:\mid{BD}\mid=\mathrm{3}\sqrt{\mathrm{5}};\:\mid{AD}\mid=\sqrt{\mathrm{13}} \\ $$$$\Rightarrow \\ $$$${r}=\frac{{abc}}{\:\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 01/Mar/22
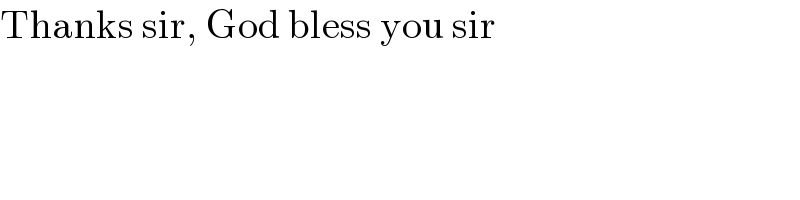
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MJS_new last updated on 04/Mar/22

$$\mathrm{yes},\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by malwan last updated on 04/Mar/22
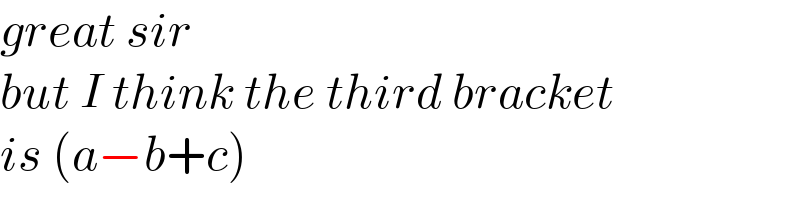
$${great}\:{sir} \\ $$$${but}\:{I}\:{think}\:{the}\:{third}\:{bracket} \\ $$$${is}\:\left({a}−{b}+{c}\right) \\ $$
