Question Number 166875 by amin96 last updated on 01/Mar/22

Commented by amin96 last updated on 01/Mar/22
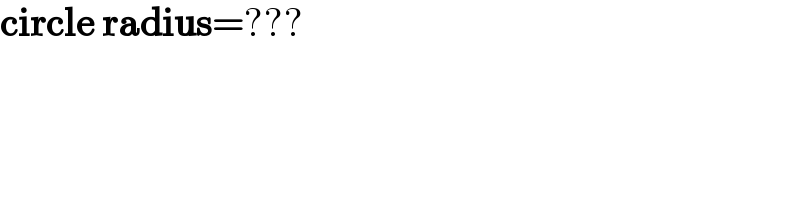
$$\boldsymbol{\mathrm{circle}}\:\boldsymbol{\mathrm{radius}}=??? \\ $$
Answered by MJS_new last updated on 01/Mar/22
![we only need the triangle with sides a=3 b=4 c=5 let the right angled vertice = the origin the circle then has the equation (x−r)^2 +(y+r)^2 =r^2 and the bevel line y=(4/3)x−4 ⇒ (x−r)^2 +((4/3)x−4+r)^2 −r^2 =0 ⇔ x^2 +((6(r−16))/(25))x+((9(r−4)^2 )/(25))=0 exactly 1 solution ⇔ Δ=0 r^2 −7r+6=0 ⇒ r=1 [the incircle of the triangle] r=6](https://www.tinkutara.com/question/Q166878.png)
$$\mathrm{we}\:\mathrm{only}\:\mathrm{need}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{sides} \\ $$$${a}=\mathrm{3}\:{b}=\mathrm{4}\:{c}=\mathrm{5} \\ $$$$\mathrm{let}\:\mathrm{the}\:\mathrm{right}\:\mathrm{angled}\:\mathrm{vertice}\:=\:\mathrm{the}\:\mathrm{origin} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{then}\:\mathrm{has}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +\left({y}+{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{bevel}\:\mathrm{line} \\ $$$${y}=\frac{\mathrm{4}}{\mathrm{3}}{x}−\mathrm{4} \\ $$$$\Rightarrow \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{3}}{x}−\mathrm{4}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{6}\left({r}−\mathrm{16}\right)}{\mathrm{25}}{x}+\frac{\mathrm{9}\left({r}−\mathrm{4}\right)^{\mathrm{2}} }{\mathrm{25}}=\mathrm{0} \\ $$$$\mathrm{exactly}\:\mathrm{1}\:\mathrm{solution}\:\Leftrightarrow\:\Delta=\mathrm{0} \\ $$$${r}^{\mathrm{2}} −\mathrm{7}{r}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\:{r}=\mathrm{1}\:\left[\mathrm{the}\:\mathrm{incircle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\right] \\ $$$$\:\:\:\:\:\:{r}=\mathrm{6} \\ $$
Commented by MJS_new last updated on 01/Mar/22
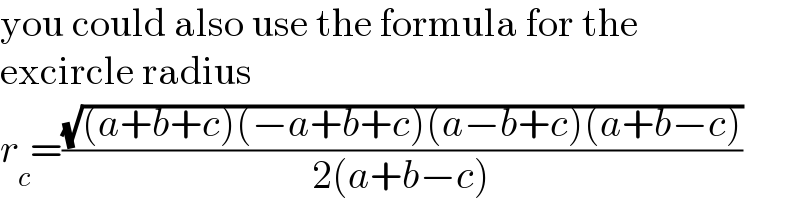
$$\mathrm{you}\:\mathrm{could}\:\mathrm{also}\:\mathrm{use}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{excircle}\:\mathrm{radius} \\ $$$${r}_{{c}} =\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{2}\left({a}+{b}−{c}\right)} \\ $$
Commented by Tawa11 last updated on 01/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 01/Mar/22

Commented by mr W last updated on 01/Mar/22

$${r}−\mathrm{3}+{r}−\mathrm{4}=\mathrm{5} \\ $$$$\Rightarrow{r}=\mathrm{6} \\ $$
Commented by Tawa11 last updated on 01/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
