Question-166911

Question Number 166911 by rexford last updated on 02/Mar/22

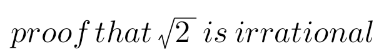
Answered by MathsFan last updated on 02/Mar/22

s u p p o s e \sqrt{2} i s r a t i o n a l

\sqrt{2} = \frac{p}{q} \Rightarrow 2 = \frac{p^{2}}{q^{2}} \Rightarrow 2 q^{2} = p^{2} \dots . . (1)

2 d i v i d e s p

2 d i v i d e s p^{2}

l e t r = \frac{p}{2} \Rightarrow p = 2 r \dots \dots . (2)

2 q^{2} = 4 r^{2} \Rightarrow q^{2} = 2 r^{2}

2 d i v i d e s q

2 d i v i d e s q^{2}

p a n d p h a v e 2 a s c o m m o n f a c t o r

b u t c o n t r a d i c t t h e f a c t t h a t p a n d q

a r e c o p r i m e

h e n c e \sqrt{2} i s a n i r r a t i o n a l n u m b e r .

Facebook Tweet Pin